|
GR0177 #2
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
fredluis
2019-08-08 06:51:12 | This seems so obvious after seeing the answer. It\'s hard to get out of the crunch mode. tree trimming |  | buaasyh
2014-10-16 20:14:04 |  , ,
take the conventional approximation 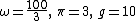 , actually it's pretty fast to get , actually it's pretty fast to get 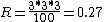 , which is a good approximation. , which is a good approximation. |  | walczyk
2012-10-06 15:52:47 | the fastest way i found was this: mrw^2 = mg*mu, approx 2pi/60 as 1/10, so w=3.33 rad/s. then assume w^2 is 10. so r=g*mu/w^2 = mu which is 0.3. |  | wittensdog
2009-10-08 16:05:46 | Here's a pretty huge coincidence that I came across when doing out this problem. Notice that, roughly,
g = 9.8067
Pi*Pi = 9.8696
Not dead-on, but when you have a problem where the answer choices are separated by factors of two, it's pretty reasonable to take:
g = Pi*Pi = 10
walczyk
2012-10-29 17:34:08 |
definitely the best way to speed this up!
|
|  | mirabzad
2009-08-03 20:53:13 | want the exact answer instead of an approximation?
The revolutions per minute is the frequency f=1/T and the period T=2*pi/w therefore w=2*pi*frequency. Setting the centripetal force equal to the frictional force gives you (mv^2)/r = umg . from v=rw => mrw^2 = umg. solving for r leads to r=ug/[(f*2*pi)^2]. using u=0.30 g=9.8 f=33.3/60 makes r=.2417 or .242 (D) which is the answer. sorry, i don't know how to use latex. |  | cherianjudy
2006-11-03 02:42:25 | Isn\\\'t it frequency(f) that is given, rather than w. Using frequency and then changing it to angular frequency will give give you a very approximate answer
a19grey2
2008-11-05 20:10:09 |
If you look at the units, I believe yosun does convert from frequency to angular frequency with the 2*pi factor.
|
|  | cherianjudy
2006-11-03 02:37:53 | |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
