|
GR9677 #93
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Potential }Potential
The problem gives a nifty potential energy graph. The period is due to each part of the potential graph.
For the simple harmonic oscillator (SHO) part, one remembers the formula 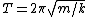 (to wit: (to wit: 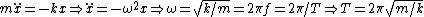 ). However, that period is for a particle to oscillate from one end of the potential curve to the other end and then back again. Since the graph shows only half of the usual SHO potential, the period contribution from the SHO part should be half the usual period: ). However, that period is for a particle to oscillate from one end of the potential curve to the other end and then back again. Since the graph shows only half of the usual SHO potential, the period contribution from the SHO part should be half the usual period: 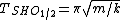
For the gravitational potential, one can calculate the period from the usual kinematics equation for constant acceleration. Recall the baby-physics equation, 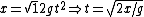 . The quantity needs to be converted to the relevant parameters of the problem. The problem supplies the constraint that the energy is constant, . The quantity needs to be converted to the relevant parameters of the problem. The problem supplies the constraint that the energy is constant, 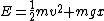 . At the endpoint, one has . At the endpoint, one has 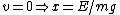 . Plugging this into the equation for time, one gets . Plugging this into the equation for time, one gets 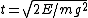 . Since the particle has to travel from the origin to the right endpoint and then back to the origin, the total time contribution from this potential is twice that, . Since the particle has to travel from the origin to the right endpoint and then back to the origin, the total time contribution from this potential is twice that, 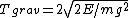 . .
The total period is thus the sum of the above contributions, which is choice (D).
|
|
|
Alternate Solutions |
QuantumCat
2014-09-18 14:37:44 | The quickest way to solve this problem, though not nearly as enlightening as Yosun's solution, is to note that part of the contribution to the period is due to half the simple harmonic potential. The only answer that has half of the period from the harmonic potential is D. |  |
|
|
Comments |
GRE1995
2016-09-26 17:55:58 | Why can you just add the periods together?nAny help is much appreciated.
whereami
2018-04-06 04:41:31 |
At x=0. Particle m has total energy = E. when it returns from either direction to this point x=0, its energy will be E. x<0 can depict a scenario in which it hit a spring at equilibrium.x>0 can depict another scenario in which it jumps into the sky and eventually comes back.
|
|  | QuantumCat
2014-09-18 14:37:44 | The quickest way to solve this problem, though not nearly as enlightening as Yosun's solution, is to note that part of the contribution to the period is due to half the simple harmonic potential. The only answer that has half of the period from the harmonic potential is D. |  | postal1248
2013-10-12 09:40:21 | If we take E=0, wouldn't the particle have no period? The only choice that satisfies this is (C) but (C) is incorrect. |  | Bonerman
2013-07-14 01:16:47 | The harmonic oscillator has angular frequency 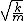 only when the total energy is initially non-zero. We expect with our potential that the frequency goes to 0 when the particle has E=0 initially so the actually frequency should be piece-wise. A small error on ETS's part I think. only when the total energy is initially non-zero. We expect with our potential that the frequency goes to 0 when the particle has E=0 initially so the actually frequency should be piece-wise. A small error on ETS's part I think. |  | faith
2010-11-02 00:11:22 | great solution yosun~ although rigorous but i bet u saw all that in less than a min~ great solution~ envious~ =) |  | vsravani
2008-11-04 18:26:24 | Why is it being stated that for x>0,
"Since the particle has to travel from the origin to the right endpoint and then back to the origin, the total time contribution from this potential is twice that, 2[sqrt(2E/mg^2)] " ?
flyboy621
2010-11-05 23:30:11 |
The calculated time is for the particle to get from the origin to its highest point. We want the time it takes to get there and back, so you double it.
However, you don't have to do this part of the problem. Everyone should recognize the left side of the potential well as a simple harmonic oscillator potential, for which the angular frequency is 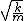 , hence the complete period is , hence the complete period is 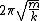 . Once you realize the left side of the well contributes half of that to the total period, (D) is the only answer that works. . Once you realize the left side of the well contributes half of that to the total period, (D) is the only answer that works.
|
|  | ssp
2008-09-07 18:24:36 | Just looking at the system and trying to find the period you need a contribution from the SHO and gravity. That eliminates (A) through (C).
Now looking at the remaining too. One is just the multiple of the other... I would take the lower multiple, as we are looking at halves not complete cycles.
Barney
2012-11-06 14:29:35 |
My thinking exactly!
|
|  | kyros
2007-11-01 21:29:48 | Observe that you can eliminate A because it has the wrong units. Now if g=0 or k = 0, the period is infinite, so our period must depend on both. Remove c and b. The period for half the oscillation for the spring is pi*root(m/k). D is the only answer which has the correct dependence. |  | Jeremy
2007-10-14 13:36:21 | The solution for the linear potential is slightly flawed. It starts with the first equation: 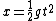 . This . This  does not represent the one used in the problem. Note the absence of an initial velocity. This equation says at time does not represent the one used in the problem. Note the absence of an initial velocity. This equation says at time 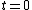 the particle is motionless at the origin; it also does not predict a turning point. What this equation is really representing is the time is takes to fall from the turning point (where the particle is motionless at the origin; it also does not predict a turning point. What this equation is really representing is the time is takes to fall from the turning point (where 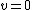 ), but in doing so it shifts the origin horizontally. They get lucky in using ), but in doing so it shifts the origin horizontally. They get lucky in using 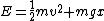 to solve for to solve for  because this equation for energy uses the original meaning of because this equation for energy uses the original meaning of  . Maybe the solution's author had all these things in mind, and this was the natural approach for them, but it's not natural at all for me. . Maybe the solution's author had all these things in mind, and this was the natural approach for them, but it's not natural at all for me.
Here's what I did: 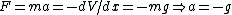 , so , so 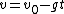 . Therefore, the time to reach the turning point ( . Therefore, the time to reach the turning point (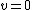 ) is ) is 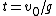 . But we know . But we know 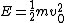 . Rearrange to get . Rearrange to get 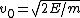 and plug into equation for and plug into equation for  . Finally, we can write down what the period . Finally, we can write down what the period 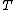 is: is: 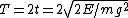 . .
Jeremy
2007-10-14 13:38:10 |
I should note that in my method 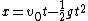 . .
|
sawtooth
2007-10-30 08:26:29 |
I dont understand why you disagree with the solution; (ok this is fine print now, but since we all love physics...) I mean, you have a point that it changes the origin, but there's no problem. We just wan to find the time it takes to get from the bottom to the top and then to the botom, and we claim that these two stages take the same time since we have energy conservation. So we use the simplest (or more natural) approach and handle zero initial velocity.
Anw, I would like to say, one ofcourse eliminates (A) due to units, then if they are to use the solution proposed here, they are sure to know that for the SHO part it will take half the expected period. So we eliminate (B) (we expect contribution due to the linear part), we eliminate (C) (we would like some k factor) and we eliminate (E) because we know it will take half of the SHO time. I know this is not that general, and some may say that a 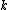 or something else could appear or disappear due to Energy conservation, but it is quite good a chance for 1.7 mins. What do you think? or something else could appear or disappear due to Energy conservation, but it is quite good a chance for 1.7 mins. What do you think?
|
timtamm
2011-08-27 11:01:56 |
Jeremy's answer is considerably more clear than Yosun's solution (to wit, I love degrading Yosun's answers)
|
Setareh
2011-10-13 01:17:36 |
I do strongly agree with Jeremy.. Because we have to notice that x=0 is not an endpoint for SHO; instead it is a central point and as we all know in SHO problems the oscillator has v=0 at endpoints. So we have to consider the initial speed at x=0 and we have to consider this fact when we want to write the baby-physics equation: x=v(0)t+1/2gt^2
|
|  | herrphysik
2006-10-13 21:01:33 | One can very quickly eliminate choices (A) and (B) because they don't have units of seconds.
buddy.epson
2006-10-14 15:24:02 |
(B) does have units of seconds. k is in kg/s^2 and m is in kg. m/k is in units of s^2 and thus sqrt(m/k) has units of sec. You are right that (A) can be eliminated by dimensional analysis, a very good point.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
