|
GR9677 #87
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Faraday Law }Faraday Law
From Faraday's Law or Len's Law, one has 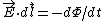 . Since, in order for the balls to move, they must move in a circle, one has . Since, in order for the balls to move, they must move in a circle, one has 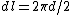 ; moreover, the induced magnetic field would point in the opposite direction to the field that was before, and one has a current in a loop from the right-hand-rule. The area of the magnetic flux is just ; moreover, the induced magnetic field would point in the opposite direction to the field that was before, and one has a current in a loop from the right-hand-rule. The area of the magnetic flux is just 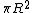 , since the field only goes through the cylindrical region of radius R. , since the field only goes through the cylindrical region of radius R.
Thus,  = \dot{B}\pi R^2 \Rightarrow E=\frac{\dot{B}R^2}{d}) . .
Now, recall some mechanics. The torque is related to the moment-arm and force by 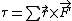 , where , where 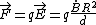 . Since there is a force contribution from each charge, and since, by the right-hand-rule, their cross-products with the moment-arm point in the same direction, one finds the torque to be . Since there is a force contribution from each charge, and since, by the right-hand-rule, their cross-products with the moment-arm point in the same direction, one finds the torque to be 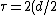q\frac{\dot{B}R^2}{d} = dq\frac{\dot{B}R^2}{d}=q\dot{B}R^2) . .
Now, recall the relation between angular momentum and torque to be  . Replace the . Replace the 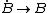 above to get above to get 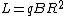 , and so the system starts rotating with angular momentum as in choice (A). (This approach is due to Matt Krems.) , and so the system starts rotating with angular momentum as in choice (A). (This approach is due to Matt Krems.)
Note that one can immediately eliminate choice (D) since angular momentum is not conserved from the external torque induced (to wit: electromagnetic induction). Moreover, although choice (E) is true in general, it does not apply to this problem.
|
|
|
Alternate Solutions |
QuantumCat
2014-09-24 18:50:29 | I did this problem in an odd way, but I got to the right answer. Hopefully someone can correct me if there's an error in my reasoning or methodology.
So this system is given to be at rest, and that means that the sum of the forces has to be zero. If you equate the centripetal force to the Lorentz force (note the centripetal force is inwardly radial, and if you consider 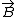 to be in the to be in the 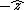 direction and direction and 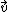 to be in the to be in the 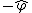 direction, the Lorentz force is outwardly radial) you can solve the problem. direction, the Lorentz force is outwardly radial) you can solve the problem.
 = = 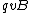
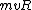 = = 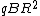
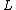 = = 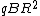
It occurred to me that I should really be using  in place of R, but for some reason this works out - I'd suspect that because in place of R, but for some reason this works out - I'd suspect that because  only "sees" a rod of radial length only "sees" a rod of radial length  . As I said, I hope someone can correct any error in this methodology, because the approach seems to be too good to be true. . As I said, I hope someone can correct any error in this methodology, because the approach seems to be too good to be true. |  | ramparts
2009-10-01 16:28:18 | Once again, limits are your friend.
Eliminating D and E by the physical means established in other answers here (that's just stuff you gotta know, or guess), you can consider  and and  going to 0 or going to 0 or  . As . As 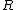 goes to zero, the magnetic field vanishes, so there should be no angular momentum. Eliminate B. As goes to zero, the magnetic field vanishes, so there should be no angular momentum. Eliminate B. As  goes to goes to  , it would make no sense (in fact, it would violate conservation of angular momentum!) if the angular momentum - or the orbital velocity - went to , it would make no sense (in fact, it would violate conservation of angular momentum!) if the angular momentum - or the orbital velocity - went to  as well, so eliminate C. That leaves A. as well, so eliminate C. That leaves A. |  | student2008
2008-10-17 09:36:12 | The electromagnetic field had the moment assosiated with the Umov-Pointing vector ![\vec S \sim [\vec E,\vec B]](/cgi-bin/mimetex.cgi?\vec S \sim [\vec E,\vec B]) , where , where 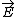 was the electorstatic field of the charges. When the magnetic field is turned off, the field moment should conserve and thus transfer into the mechanical momentum of our system. Then, one may notice that as was the electorstatic field of the charges. When the magnetic field is turned off, the field moment should conserve and thus transfer into the mechanical momentum of our system. Then, one may notice that as 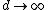 , , 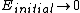 , so , so 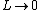 or at least or at least 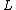 is limited. Only the answer (A) works this way. is limited. Only the answer (A) works this way. |  | shoyer
2007-08-05 23:27:36 | There is an easier way to solve this problem.
First, you can eliminate E because even though magnetic forces do no work, that doesn't mean they can't cause systems to move. The rod rotating would not be in a higher energy state.
Answers A-C assume there was angular momentum stored in the field -- answer D claims otherwise. I wasn't entirely sure about eliminating D but it didn't feel right (I wasn't sure about the induced force but that explanation in the official answer makes sense).
Unlike the official answer, I'm considering the momentum of the entire system. In that case, since the magnetic field's size has nothing to do with the positions of the balls, the stored momentum in that field should not be dependent on d. This eliminates B and C, leaving A as the answer. |  |
|
|
Comments |
buaasyh
2015-10-07 13:29:58 | According to Faraday\'s law, E*Pi*d=d Phi/d t. Thus E = (d Phi/d t)/(Pi*d). The force acting on the two pith balls is E*q. Then the corresponding torque is E*q*d/2. Two pith balls contribute twice the torque as E*q*d=q*(d Phi/d t)/Pi. Integrate both sides with respect to t over the process, we have the angular momentum of the system is q times the total change of the magnetic flux over Pi which is q*B*Pi*R^2/Pi=q*B*R^2. |  | QuantumCat
2014-09-24 18:50:29 | I did this problem in an odd way, but I got to the right answer. Hopefully someone can correct me if there's an error in my reasoning or methodology.
So this system is given to be at rest, and that means that the sum of the forces has to be zero. If you equate the centripetal force to the Lorentz force (note the centripetal force is inwardly radial, and if you consider 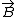 to be in the to be in the 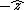 direction and direction and 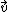 to be in the to be in the 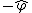 direction, the Lorentz force is outwardly radial) you can solve the problem. direction, the Lorentz force is outwardly radial) you can solve the problem.
 = = 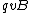
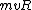 = = 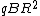
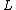 = = 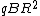
It occurred to me that I should really be using  in place of R, but for some reason this works out - I'd suspect that because in place of R, but for some reason this works out - I'd suspect that because 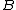 only "sees" a rod of radial length only "sees" a rod of radial length 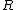 . As I said, I hope someone can correct any error in this methodology, because the approach seems to be too good to be true. . As I said, I hope someone can correct any error in this methodology, because the approach seems to be too good to be true.
dipanshugupta
2017-03-23 14:14:43 |
Isn\\\\\\\'t the charge outside the region magnetic field is incident?
|
capoo0819
2017-10-27 12:50:22 |
This might be the special case which 2R=d, thus the answer would still be correct.
|
|  | ndminh1990
2013-09-26 20:22:19 | This is the case of curl field, so E is incorrect. D is also incorrect since the the field B does contain energy. Simply let $d -> \infty,$ only A is reasonable. |  | fpaslan
2011-10-22 13:28:49 | I thought as follows;
When the magnetic field is turned off, the charges try to create the same magnetic field by rotating. With the creation of the B, the equation,
qvB=mv^2/R is satisfied.
We can obtain the L from this equation;
qBR=mv
mvR=qBR^2.
There is no dependence on d but R, since the B is constrained in the region with the area (pi)R^2. |  | faith
2010-10-21 20:55:29 | i think there another method, took me bout a gud 5 secs out of luck i think
L=mvR ------1
F=qvb=mv^2/R-------2
solve equation 2 for v plug in 1. end
is this right? i assume that two particles at rim on R distance on rod. since its the maximum distance that it can for it to rotate.
flyboy621
2010-11-05 22:32:55 |
They say it's better to be lucky than good.
You were lucky.
|
|  |
2010-03-19 13:17:57 | Imagine the motion of a single particle in a B-field. The linear momentum,  . Angular momentum, . Angular momentum,  . (A) . (A)
What is wrong with this solution? |  | cilginfizikci
2010-03-09 01:06:55 | For the solution at the top: The induced magnetic field direction can not be opposite to what it was before... on the contrary it s the same direction, so that the magnetic flux will be kept constant... Len'z law says that the closed loops doesnt like the change in magnetic flux... there was a magnetic field at the beginning and hen suddenly it s gone so is the magnetic flux... the two cgarhe system will begin rotating to acquire the former magnetic flux value... This approach looks the most formal one, and i tried to solve in this way, however the angular momentum i found is ( mdB(pi^2)(R^2) )/q u0 .... so i dunno what was the guy who prepared this question was thinking... |  | ramparts
2009-10-01 16:28:18 | Once again, limits are your friend.
Eliminating D and E by the physical means established in other answers here (that's just stuff you gotta know, or guess), you can consider 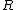 and and  going to 0 or going to 0 or  . As . As 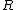 goes to zero, the magnetic field vanishes, so there should be no angular momentum. Eliminate B. As goes to zero, the magnetic field vanishes, so there should be no angular momentum. Eliminate B. As  goes to goes to  , it would make no sense (in fact, it would violate conservation of angular momentum!) if the angular momentum - or the orbital velocity - went to , it would make no sense (in fact, it would violate conservation of angular momentum!) if the angular momentum - or the orbital velocity - went to  as well, so eliminate C. That leaves A. as well, so eliminate C. That leaves A.
fjornada
2009-10-19 14:28:30 |
nice!!
|
mike
2009-11-06 16:45:45 |
this is the best way of doing it
|
kronotsky
2018-10-22 04:03:09 |
More simply, the angular momentum comes from the magnetic field, so it cannot depend on d.
|
|  | student2008
2008-10-17 09:36:12 | The electromagnetic field had the moment assosiated with the Umov-Pointing vector ![\vec S \sim [\vec E,\vec B]](/cgi-bin/mimetex.cgi?\vec S \sim [\vec E,\vec B]) , where , where 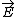 was the electorstatic field of the charges. When the magnetic field is turned off, the field moment should conserve and thus transfer into the mechanical momentum of our system. Then, one may notice that as was the electorstatic field of the charges. When the magnetic field is turned off, the field moment should conserve and thus transfer into the mechanical momentum of our system. Then, one may notice that as 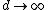 , , 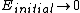 , so , so 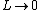 or at least or at least 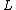 is limited. Only the answer (A) works this way. is limited. Only the answer (A) works this way. |  | casaubon
2008-10-04 18:19:31 | where does this dl come from in Faraday's law?rnrnEverything I see just has 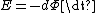 , why is it , why is it 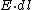 now? now?
casaubon
2008-10-15 18:34:57 |
so to address my own question,
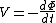
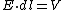
|
|  | p3ace
2008-05-05 01:36:02 | This is an interesting problem. Lenz's Law is easy to brush off as just explaining the minus sign in Faraday's law, but it really should be given more emphasis. One cannot determine the direction without understanding what the minus sign really means. If the change in B is an increase in B then the induced field opposes the original direction of B, but if the change in B is a decrease, then the direction is IN THE SAME DIRECTION AS B. |  | p3ace
2008-04-11 13:49:21 | To answer my own question, I suppose that it is the induced electric field that actually does the work, and not the magnetic field that did the inducing, although, the work wouldn't get done with out the change in the B field. I suppose that what ever caused the change in the B field did the original work. |  | p3ace
2008-04-11 13:44:37 | Also, if magnetic forces do no work, then why is W=(1/2)Li^2? |  | p3ace
2008-04-11 13:33:24 | Since the magnitude is all that is asked for in this problem, it doesn't matter, but the direction doesn't oppose the direction of the original B field. It opposes the change, whatever direction that is. If the change in B is a decrease, the change is in the opposite direction of B. Thus, the induced B field is in the same direction as the original B, which is opposite the change.
Another thing is, at first I was thinking about a current being induced with the axis of rotation downward so that the charges circulate from right to left on the near side. This is one way to look at it. When I think of angular momentum, I think of it having mass, and in this case it doesn't, which is a little confusing. |  | bkardon
2007-09-30 09:44:17 | This is just a tripped up magnetic induction problem, like problem #2. When you take away the magnetic flux, you will induce a current in the "pith" balls; i.e. you will make the rotate. Without doing much work, you know that the voltage is proportional to the change in flux, which is dependent on R^2. We can also safely assume that the angular momentum is not related to d, since the angular momentum induced shouldn't be dependent on the arrangment of charges carrying it. This indicates choice A.
|  | shoyer
2007-08-05 23:27:36 | There is an easier way to solve this problem.
First, you can eliminate E because even though magnetic forces do no work, that doesn't mean they can't cause systems to move. The rod rotating would not be in a higher energy state.
Answers A-C assume there was angular momentum stored in the field -- answer D claims otherwise. I wasn't entirely sure about eliminating D but it didn't feel right (I wasn't sure about the induced force but that explanation in the official answer makes sense).
Unlike the official answer, I'm considering the momentum of the entire system. In that case, since the magnetic field's size has nothing to do with the positions of the balls, the stored momentum in that field should not be dependent on d. This eliminates B and C, leaving A as the answer.
evanb
2008-07-02 13:50:36 |
See Griffith's page 358.
However, the stored momentum is dependent on 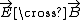 , so the stored momentum could be dependent on d, through , so the stored momentum could be dependent on d, through  . .
|
ramparts
2009-10-01 16:25:53 |
If you don't have Griffiths on hand, what that page says is that as long as 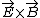 is non-zero, the field contains energy and angular momentum, even if the system is static :) is non-zero, the field contains energy and angular momentum, even if the system is static :)
|
|  | vinograd19
2007-02-02 10:00:05 | There is no fields around balls. Thus there is no forces to move it.
lukassvec
2007-07-25 00:21:28 |
I though so to in the beginning but then again, there is an electric field inside the magnetic field.
|
newton
2007-09-27 21:19:17 |
a changing magnetic field creates an electric field-Faradays law
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
