GREPhysics.NET: GR9677 #79

GR9677 #79

Problem

GREPhysics.NET Official Solution

This problem is still being typed.

Statistical Mechanics $\Rightarrow$ }Specific Heat

The specific heat at constant volume for high temperatures is $c_v = 7/2 R$ . The specific heat at low temperatures is $3/2 R$ . Why?

There are three contributions to the specific heat of a diatomic gas. There is the translational, vibrational, and rotational. At low temperatures, only the translational heat capacity contributes $U = 3/2 N k T \approx c_v T \Rightarrow c_V=3/2 Nk$ . At high temperatures, all three components contribute, and one has $c_V=(3/2+1+1)Nk = 7/2 Nk$ .

The general formula is $c_v = c_v(translational)+c_v(rotational)+c_v(vibrational)=Nk\left(3/2 + 1 + (h\nu/(k\theta))^2 \exp(h\nu/(k\theta))/(\exp(h\nu/(k\theta))-1)^2 \right)$

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

bluejay27
2016-12-25 22:22:27

Check page 606 and 607. D is the correct answer.

bluejay27
2016-12-25 22:22:53

of Young and Freedman

Reply to this comment

hellothar
2012-10-21 20:26:23

No one seems to have pointed out that Cv, for a DIatomic gas, at low temperatures is not 3/2R but 5/2R. (Check HRK, or Fermi, or anywhere else).

Yosun's 3/2R applies only to monoatomic molecules. The problem asks about diatomic molecules.

hellothar
2012-10-21 20:33:06

Nope. Nevermind. The standard texts are assuming only 3+2 vibrational modes. For very, very low temperatures, 3/2 is right.

Reply to this comment

shafatmubin
2009-11-04 15:17:49

This link might help:

http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html

It shows the variation of Cv of hydrogen gas with temperature. At very high temperatures, above 1000 K, there are 7 degrees of freedom because two additional degrees (apart from the 3 translational and 2 rotational degrees) become active. Can anyone explain what are these two new degrees of freedom? One of them is possibly vibrational, but what about the other?

hdcase
2009-11-04 21:46:12

Hyperphysics doesn't make this very clear, but wikipedia does:
http://en.wikipedia.org/wiki/Specific_heat_capacity#Diatomic_gas

The vibrational state (there is one degree of freedom from it, for a total of 6 degrees of freedom) adds R (instead of R/2) because it carries both a potential and kinetic term (both of which can "hold energy," which is essentially what the specific heat measures).

shafatmubin
2009-11-05 13:12:22

Thanks hdcase. Vibrational energy contributing R instead of 2R makes things a lot more understandable.

Reply to this comment

petr1243
2008-03-18 11:45:15

Roughly, Rotaional effects disappear below 25k, and all 3 effects will produce a specific heat of 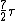$\frac{7}{2}\tau$ at temperatures above 8000K. A good reference is ch.18 of the University Physics text.

Reply to this comment

cyberdeathreaper
2007-02-03 15:05:37

I found this equation helpful in solving the problem:

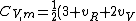$C_{V,m} = \frac{1}{2} (3 + v_R + 2v_V)R$

Where

$v_R = 2$

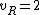
for linear molecules, and

$v_R = 3$

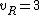
for non-linear molecules.

I assumed that that

$v_V = 1$

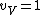
for very high temperatures. And of course, the rotational and vibrational contributions are 0 at very low temperatures, as Yosunism explained in the answer.

faith
2010-11-11 20:24:18

equipartition says each degree of freedom has 0.5 K.E.

translational has 3 mode of d.f

rotational
for diatomic ( linear) 2 mode
triatomic has 3x2 mode =6
polyatomic 3 mode (why ? i do not know)

vibrational (i need help completing this)
diatomic = 1 (or 2) mode?
triatomic=?
poly=?

to the question
finding the df for high tem
1/2(3+2+1?)=1?
if its vibrational has 2 mode: 1/2(3+2+2)=7/2

so the answer could be D or E. any formula for vibrational mode under high temp?

Reply to this comment

Post A Comment!

You are replying to:

I found this equation helpful in solving the problem:
$C_{V,m} = \frac{1}{2} (3 + v_R + 2v_V)R$
Where
$v_R = 2$
for linear molecules, and
$v_R = 3$
for non-linear molecules.
I assumed that that
$v_V = 1$
for very high temperatures. And of course, the rotational and vibrational contributions are 0 at very low temperatures, as Yosunism explained in the answer.

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone