|
GR9677 #69
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Ampere Law }Ampere Law
Recall Ampere's Law, 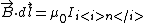 . .
Since the region one is interested in is a vacuum, one's Ampere Loop encloses all of the current. Thus, the field from each conductor is  = \mu_0 J \pi R^2) , where, , where, 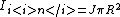 and R is the radius of the conductor. (This is a good approximation of the current, as one assumes that the vacuum region in the center is small compared to the area of the conductors.) and R is the radius of the conductor. (This is a good approximation of the current, as one assumes that the vacuum region in the center is small compared to the area of the conductors.)
Making the approximation that 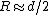 , one has , one has 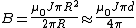 . Since both fields contribute in the center, the field is twice that, . Since both fields contribute in the center, the field is twice that, 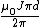 , as in choice (A). , as in choice (A).
(Also, one can immediately eliminate all but choices (A) and (B) by the right-hand rule. One seeks a +y-direction field.)
|
|
|
Alternate Solutions |
djh101
2014-09-22 21:45:53 | Ampere's Law. Take r to be d/2 (the distance to A) and ignore the vacuum, since it will go away when you un-superpose the two wires.
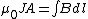
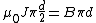
Multiply by 2 and rearrange to get answer A. |  | phoxdie
2010-11-10 17:12:20 | This sort of problem is usually very intimidating to me when taking these practice tests. After looking at it a bit more I realized it really wasn't that difficult and you dont need to know alot of EM to solve it. Start simply with the right hand rule and you find that only A and B are correct answers (it is possible that E could be right but unlikely based on result of RHR.) If you are like me you probably forgot how to solve this with some amount of formalism, so instead consider limits!!
Start with choice B, if  becomes becomes 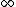 small this suggests that the small this suggests that the 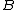 field with grow field with grow 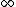 large which can't be right, and we can pick A as the right answer. large which can't be right, and we can pick A as the right answer. |  | Richard
2007-10-01 18:35:55 | One should note that by geometry there will be no dependence on the radius r in the solution:
Thus (a) is the answer.
|  | sharpstones
2006-11-30 12:23:41 | It would be easier to not consider any vacuum in the center. Since you have current flowing in opposite directions they will naturally cancel each other out in the middle. Simple find the field at A due to one of the cylinders of current(it will be a distance d/2 from the center) and then multiply times 2. |  |
|
|
Comments |
amber
2014-10-20 12:36:17 | I think this is the best answer because if you plug in d = 2r both A and B depend on r. The only difference is a factor of 2: answer B is twice that of A.
Quick and easy |  | djh101
2014-09-22 21:45:53 | Ampere's Law. Take r to be d/2 (the distance to A) and ignore the vacuum, since it will go away when you un-superpose the two wires.
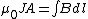
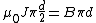
Multiply by 2 and rearrange to get answer A.
djh101
2014-09-22 21:46:48 |
Sorry, that d/2 on the left should be squared.
|
|  | physicsphysics
2011-10-11 08:05:46 | Does anybody concentrate the "conductor"? Because the center is rounded by the conductor, I think the center should be zero. What am I wrong? |  | phoxdie
2010-11-10 17:12:20 | This sort of problem is usually very intimidating to me when taking these practice tests. After looking at it a bit more I realized it really wasn't that difficult and you dont need to know alot of EM to solve it. Start simply with the right hand rule and you find that only A and B are correct answers (it is possible that E could be right but unlikely based on result of RHR.) If you are like me you probably forgot how to solve this with some amount of formalism, so instead consider limits!!
Start with choice B, if  becomes becomes 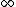 small this suggests that the small this suggests that the 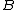 field with grow field with grow 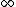 large which can't be right, and we can pick A as the right answer. large which can't be right, and we can pick A as the right answer. |  | The_Duck
2010-07-05 15:35:29 | If you can convince yourself that there is a magnetic field, and that the pi in pi r^2 cancels the pi in u_0/4pi, that alone gives you A (since B,C,D all have factors of pi. Also note that there's no answer with a factor of pi^2, so the pi's must cancel).
The_Duck
2010-07-05 15:41:02 |
Actually I think above my identification of the source of the pi's is wrong but the reasoning should still apply.
|
|  | bucky0
2007-10-02 19:22:28 | Don't the fields cancel? If the currents are equal traveling in each direction, you should end up with the same B field contribution from each side, but in opposite directions, which would drop it to zero, correct?
antithesis
2007-10-04 20:48:53 |
But one is on the right of A, and one is to the left, so that they add up (think of right hand rule)
|
|  | Richard
2007-10-01 18:35:55 | One should note that by geometry there will be no dependence on the radius r in the solution:
Thus (a) is the answer.
ewhite2
2007-10-30 18:57:02 |
why?
|
FortranMan
2008-08-29 12:47:04 |
because increasing the radius, while increasing the distance between their centers, would also increase the current, hence the answer should not be proportional to the inverse of r. Only d really matters in the magnitude of the field.
|
hanin
2009-09-29 22:37:52 |
Why increasing radius would also increase current? I imagine this like 2 pipes carrying water; no matter how much you enlarge your your pipe, the same amount of water will always flow if there is no change in the source.
|
dogsandfrogs
2009-10-08 12:24:51 |
Current is given as a current density, not a set value. Density is the same regardless of r, hence why the answer should not depend on r.
|
alemsalem
2010-09-28 07:16:03 |
because of Ampere's law, only Ienc can contribute to the magnetic field, draw a circle from the center to point A, then you can draw any concentric circle of bigger radius (r) which will not contribute to the magnetic field at A, you can do the same to the other conductor, and because of the principle of superposition you just add the 2 contributions.rnI hope I made sense.
|
|  | sharpstones
2006-11-30 12:23:41 | It would be easier to not consider any vacuum in the center. Since you have current flowing in opposite directions they will naturally cancel each other out in the middle. Simple find the field at A due to one of the cylinders of current(it will be a distance d/2 from the center) and then multiply times 2.
flyboy621
2010-11-02 22:25:55 |
That's a great point. Looking at it that way, you can clearly see that the portion of the current we care about is only the part that is less than d/2 from the center of each "wire."
You don't even have to do any calculations if you realize the field must be in the +y direction and does not depend on r.
|
amber
2014-10-20 12:34:43 |
I think this is the best answer because both A and B (if you plug in d=2r) depend on the radius r. The only difference is a factor of two. answer B is twice answer A.
|
|  | santon
2006-11-02 15:08:53 | |  | yosun
2005-11-11 21:24:16 | keflavich: thanks for the typo-alert; it has been corrected. |  | keflavich
2005-11-11 18:27:43 | Typo: "All but choices A and B because they have a +y field" should probably replace the last thing in parentheses. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
