rabia
2012-10-11 01:04:05 | I have to solve a problem by using Coulumn' law given rho=rho not (1-r/R) and find Q from given expression. | 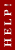 |
physicsphysics
2011-10-11 07:22:32 | Does anybody have a problem by using Coulumn' law?
I used  . The answer is . The answer is 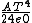 . Can anybody explain what I am wrong? . Can anybody explain what I am wrong?
3Danyon
2011-10-13 08:44:10 |
I made the same mistake initially. The thing is, one has to calculate the charge first and then divide by the ^2) . Otherwise you change the integrand and get the wrong numerical factor. To spell it out, the field is given by: . Otherwise you change the integrand and get the wrong numerical factor. To spell it out, the field is given by:
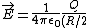^2} = \frac{1}{4\pi \epsilon_0 (R/2)^2} \cdot \int (A r^2) \cdot r^2 \sin{\theta} dr d\theta d\phi )
|
|  |
phoxdie
2010-11-10 15:20:06 | Sorry to get hung up on this, but it was very confusing the first time I looked at this solution. There is a small "typo" in the solution. A factor of epsilon is dropped for no reason. |  |
Kabuto Yakushi
2010-09-19 10:28:26 | Another method for solving this problem would be to take the volume integral of  to solve for Q. Then to plug Q into Gauss' law. to solve for Q. Then to plug Q into Gauss' law.

where 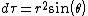drd{\theta}d{\phi})
plug Q into Gauss' law:
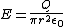
solving one gets choice B).
Yosun's solution is faster, but if using the shell method for integration doesn't come to mind, one must resort to the long method. |  |
tsharky87
2009-11-06 08:46:03 | I was confused about the fact that I seemed to be getting a  , so here's an explanation for those of you who were as confused as azot and I: , so here's an explanation for those of you who were as confused as azot and I:
I was getting my r's confused in Yosun's solution, I just took 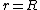 and canceled away. The reason this is wrong is that the radius that you are taking the area with when multiplying by and canceled away. The reason this is wrong is that the radius that you are taking the area with when multiplying by  is actually is actually 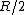 . So if you set . So if you set 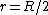 you should arrive at the solution. you should arrive at the solution. | 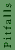 |
jw111
2008-11-05 15:43:14 | in addition, if you set A=1, R=1, epsilon=1
it will be easier

then
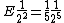
E= 1/40
pam d
2011-09-17 16:24:27 |
nice
|
|  |
gliese876d
2008-10-11 20:56:52 | hmm. I'm just wondering... I had the following formula memorized for similar situations:
E=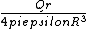
Where little r is the radius of the point from the center and R is the total radius of the sphere
Now using this formula I figured Q would equal 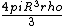
so I used this in the numerator for Q and also plugged in r= R/2 and you get
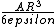
which is *close* to the right answer, but not quite... where does this standard formula fall apart in reasoning for this particular situation?
flyboy621
2010-11-02 21:12:58 |
I think you are assuming constant charge density, which is not the case here.
|
|  |
hisperati
2007-10-31 20:29:18 | To find the charge we need to integrate a charge density, that is per unit volume. The answers correspond to multipliying by a surface area ( I am not talking about the left side of Guass's Law, where it is obvious surface area is correctly used). Why isn't the charge density multiplied by  ? ?
blah22
2008-03-14 18:01:46 |
Yea I'm confused too
|
blah22
2008-03-14 18:27:59 |
Ah I see, for anyone else confused by this in the future, it's just a method of getting the volume of a sphere through integration. Divide the sphere into lots of shells of thickness dr, each with surface area  . .
Thanks so much Yosun!
|
flyboy621
2010-11-02 21:14:34 |
You can't just multiply the charge density by the enclosed volume because the density is not constant. You have to integrate.
|
|  |
azot
2007-10-23 06:04:01 | the answer to this problem is wrong .
E shoud be equal to A*R^3/32*5
azot
2007-10-23 06:05:00 |
sorry I was wrong :) Everything is ok
|
kevinjay15
2007-10-23 18:24:01 |
ETS is never wrong.
|
|  |
