|
GR9677 #62
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Capacitors }Capacitors
 Initially, one has the two capacitors connected in parallel, so that each receives the same voltage from the battery. Thus
Initially, one has the two capacitors connected in parallel, so that each receives the same voltage from the battery. Thus 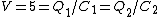 . . 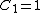 and and  , thus , thus 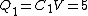 and and 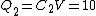 . .
After the battery is removed and the capacitors are re-connected so that the opposite plates face each other, one has (immediately) 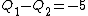 . The charges would then redistribute themselves so that the voltage across each capacitor is the same. Thus, denoting the final charge on each capacitor as . The charges would then redistribute themselves so that the voltage across each capacitor is the same. Thus, denoting the final charge on each capacitor as 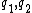 , respectively, one has (from charge conservation) , respectively, one has (from charge conservation) 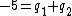 . Applying the equi-voltage condition, one has . Applying the equi-voltage condition, one has  . Plug that into the charge conservation equation to get . Plug that into the charge conservation equation to get 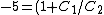q_2\Rightarrow q_2=3.33 \Rightarrow V=q_2/C_2 \approx 1.7) , as in choice (C). (As an exercise, one can also check by computing the charge for the other capacitor.) , as in choice (C). (As an exercise, one can also check by computing the charge for the other capacitor.)
|
|
|
Alternate Solutions |
Barney
2012-11-06 11:29:39 | Initially we havern 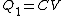 rn rn 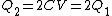 rntotal charge on bothrn rntotal charge on bothrn 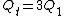 rnCombining capacitors with oppositely charged ends rnCombining capacitors with oppositely charged ends 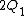 of charge cancel, of charge cancel, 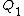 of charge redistributes on both capacitors.rnElectrons occupy the area across plates of both capacitors in equal density, thus of charge redistributes on both capacitors.rnElectrons occupy the area across plates of both capacitors in equal density, thus 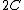 compared to compared to 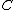 is just twice as much area, thus twice as many electrons. ( is just twice as much area, thus twice as many electrons. (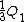 of all electrons on of all electrons on 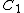 opposed to opposed to  of all electrons on of all electrons on 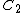 )rnFinally, the initial 5 V relate to the searched )rnFinally, the initial 5 V relate to the searched  V the same as the initial charge of V the same as the initial charge of 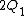 relates to final charge of relates to final charge of  .rnThat gives:rn .rnThat gives:rn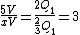 rnTherefore, new voltage:rn rnTherefore, new voltage:rn |  | ezfzx
2012-10-06 21:53:23 | Don't think about the capacitor circuit as a set of capacitors ... think of it as a set of seperated pieces of conductors in close proximity, nearly making contact at the locations we "call" capacitors. A battery in the circuit can also be thought of as two pieces of conductor for this thought experiment.
I believe the capacitors are considered in parallel because after the connection, there are only two pieces of conductor. If they had been in series, there would need to be at least three (with the stray ends either not connected, or connected to something else). |  | troy12345
2006-10-25 20:40:48 | There's an even simpler way to do the problem: The charge stored on C1 is Q1 = V*C1. Similarly, Q2=V*C2. Now when the capacitors are rearranged, they are still in parallel as the voltage across each must be the same due to Kirchoff's Voltage Rule. Hence, we can construct an equivalent capacitor with capacitance Ceq = C1 + C2. Since plates of opposite charge connected, the total charge stored on the equivalent capacitor is Qeq = Q2-Q1 = V(C2-C1). The voltage across the capacitor is Veq = Qeq/Ceq = V(C2-C1)/(C1+C2) = 1.667 V (Choice C).
nitin
2006-11-02 22:20:42 |
The capacitors are not in parallel, but in series, when one capacitor's positive plate is connected to the other's negative plate.
|
barefoot0
2006-11-05 07:56:51 |
After the initial neutralization or Q1-Q2, The plates are essentialy in parralel. The charge on either end will match for both capacitors.
This is the way I would do it.
|
barefoot0
2006-11-05 07:57:40 |
I said charge in my last post but I meant voltage.
|
|  |
|
|
Comments |
djh101
2014-09-21 12:59:26 | "Charging a capacitor" means that the capacitor is attached to a voltage source and charged, like a battery. The point here is that the capacitor will be fully charged when it is attached to the other capacitor. The capacitor is charged to 5V. It's perfectly possible that the capacitors were charged at different times or with different voltage sources, all that matters is that they are at 5V at the second part of the question. Series and parallel are irrelevant. |  | medhavijosh@gmail.com
2014-01-12 23:02:46 | as the total charge on the capacitors is 5uC and the equivalent capacitance is 3uF as voltage on both capacitor is same so voltage across 2uF capacitor is=5/3=1.7V
|  | Jovensky
2013-09-24 11:29:30 | I think it doesn't matter if the capacitors are initially connected in series or parallel. I did the problem assuming it was connected in series.
Then after disconnecting and connecting the capacitors again, the voltage will stay the same as they are in series again.
This gives the correct answer. |  | Barney
2012-11-06 11:29:39 | Initially we havern 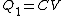 rn rn 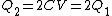 rntotal charge on bothrn rntotal charge on bothrn 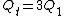 rnCombining capacitors with oppositely charged ends rnCombining capacitors with oppositely charged ends 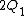 of charge cancel, of charge cancel, 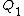 of charge redistributes on both capacitors.rnElectrons occupy the area across plates of both capacitors in equal density, thus of charge redistributes on both capacitors.rnElectrons occupy the area across plates of both capacitors in equal density, thus 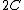 compared to compared to 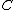 is just twice as much area, thus twice as many electrons. ( is just twice as much area, thus twice as many electrons. (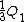 of all electrons on of all electrons on 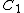 opposed to opposed to  of all electrons on of all electrons on 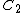 )rnFinally, the initial 5 V relate to the searched )rnFinally, the initial 5 V relate to the searched  V the same as the initial charge of V the same as the initial charge of 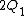 relates to final charge of relates to final charge of  .rnThat gives:rn .rnThat gives:rn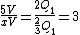 rnTherefore, new voltage:rn rnTherefore, new voltage:rn |  | ezfzx
2012-10-06 21:53:23 | Don't think about the capacitor circuit as a set of capacitors ... think of it as a set of seperated pieces of conductors in close proximity, nearly making contact at the locations we "call" capacitors. A battery in the circuit can also be thought of as two pieces of conductor for this thought experiment.
I believe the capacitors are considered in parallel because after the connection, there are only two pieces of conductor. If they had been in series, there would need to be at least three (with the stray ends either not connected, or connected to something else). |  | synthetic
2011-11-06 12:50:57 | here is how you do this problem in 2 seconds.
the 5V will be distributed across the two capacitors now. The smaller one will carry the large voltage and thus you just multiply 5V* 1/3 where 1 is the capacitance of the smaller capacitor and 3 is the sum of the two capacitors. It's the GRE people, you don't have all day.
It's a ration problem, as it always is with 2 capacitors or 2 resistors, etc.
5/3=1.7
twinkling
2012-10-14 06:36:35 |
arnt we asked to find potential across 2 microfarad capacitor??????/
|
twinkling
2012-10-14 06:37:01 |
arnt we asked to find potential across 2 microfarad capacitor??????/
|
|  | pam d
2011-09-17 17:05:33 | This one is tricky if you think you can use energy conservation due to the lack of a resistive element. This does not appear to work if you calculate the energy stored before and after they are connected. Charge conservation is the way to go.
pam d
2011-09-17 17:10:52 |
"With resistive wires." Damn it.
|
|  | his dudeness
2010-07-22 11:13:46 | The capacitance basically tells you how much charge a capacitor can hold to sustain a given voltage. Initially, C1 holds 5 uC while C2 holds 10 uC. So there is 15 uC to go around, and C2 holds 2/3 of it. rnrnNow, when opposite plates are connected, there is only 10-5=5 uC to go around. Clearly the ratio of charge held by C2 and C1 will still be the same. But since there is only 1/3 as much total charge to go around, C2 will hold 1/3 as much charge as it did originally, and will therefore have 1/3 its initial voltage. And boom goes the dynamite.
nontradish
2012-04-19 12:36:27 |
I like this solution! Quick and easy!
|
|  | his dudeness
2010-07-22 11:13:14 | The capacitance basically tells you how much charge a capacitor can hold to sustain a given voltage. Initially, C1 holds 5 uC while C2 holds 10 uC. So there is 15 uC to go around, and C2 holds 2/3 of it. rnrnNow, when opposite plates are connected, there is only 10-5=5 uC to go around. Clearly the ratio of charge held by C2 and C1 will still be the same. But since there is only 1/3 as much total charge to go around, C2 will hold 1/3 as much charge as it did originally, and will therefore have 1/3 its initial voltage. And boom goes the dynamite. |  | rawr
2009-09-25 19:41:18 | This question is horribly worded. There should be a diagram associated with it. It is unclear whether they are connected in series (which yields answer (D) ) or in parallel (which yields answer (C)). Opposite charges touching implies series, which apparently is not correct. How is anyone supposed to figure that out using equivalent capacitance?
faith
2010-11-01 23:43:38 |
AGREED!! ambiguous!!
|
djh101
2014-09-21 12:50:43 |
They are connected to each other (one to the other), there is no circuit involved. Series/parallel implies that their is a circuit and, if there was, the capacitors would discharge and V would be 0.
|
|  | p3ace
2008-04-11 09:01:43 | The way ETS worded this problem doesn't say that the capacitors are connected in parallel to each other when they are being charged. It just says each one has been charged using 5V. One would have to assume that they are in parallel for the equi-voltage thing to apply. That's why I think that this problem should be thrown out!!!!!!!!!! La, la, la, la |  | antithesis
2007-10-04 20:36:02 | I tried to do this slightly different, I know I'm at least partly right, I just can't figure out something towards the end (Using micro on all C and Q units)
After finding they have charge of 10 and 5, I'm saying after you flip one around, the new total charge is 5 (and not -5).
Since they are in series, the charge is going to split according to the capacitance, so 2/3 of the charge goes to the 2.0 capacitor, which is 10/3 C. now use 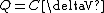 , so , so 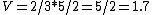
So far so good.
Now, if, instead of finishing as I did above, I first tried this, and I keep getting a wrong answer.
The net capacitance of the two in series is 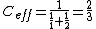 . Let's now compute total voltage across both capacitor. Total charge is 5, so . Let's now compute total voltage across both capacitor. Total charge is 5, so 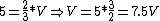 . There is no way the total voltage across both can be so high. . There is no way the total voltage across both can be so high.
Any clue what I'm doing wrong in this second method? I've been running around this in circles, and I can't see my mistake. Thanks!
Jeremy
2007-10-18 12:04:58 |
The voltage across one of the capacitors will be the same as the voltage across the other - the capacitors are connected in parallel. (Think about how you would measure the voltage being asked for, and you'll see that your measuring device sees the capacitors in parallel.) So 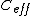 is 3, not 2/3. is 3, not 2/3.
|
sawtooth
2007-10-29 04:53:39 |
antithesis, by saying 2/3 of the charge goes to the 2μF Capacitor you imply that total capacitance is 3μF, so you ARE using the fact that they are still connected in parallel (after the charge has been rearranged). Why do you need to try another method? (Second part of your post).
|
|  | troy12345
2006-10-25 20:40:48 | There's an even simpler way to do the problem: The charge stored on C1 is Q1 = V*C1. Similarly, Q2=V*C2. Now when the capacitors are rearranged, they are still in parallel as the voltage across each must be the same due to Kirchoff's Voltage Rule. Hence, we can construct an equivalent capacitor with capacitance Ceq = C1 + C2. Since plates of opposite charge connected, the total charge stored on the equivalent capacitor is Qeq = Q2-Q1 = V(C2-C1). The voltage across the capacitor is Veq = Qeq/Ceq = V(C2-C1)/(C1+C2) = 1.667 V (Choice C).
nitin
2006-11-02 22:20:42 |
The capacitors are not in parallel, but in series, when one capacitor's positive plate is connected to the other's negative plate.
|
barefoot0
2006-11-05 07:56:51 |
After the initial neutralization or Q1-Q2, The plates are essentialy in parralel. The charge on either end will match for both capacitors.
This is the way I would do it.
|
barefoot0
2006-11-05 07:57:40 |
I said charge in my last post but I meant voltage.
|
pkamal
2010-10-02 20:43:17 |
I don't see how the capacitors are parallel.
|
ali8
2011-07-28 04:44:09 |
I, too, don't see how the capacitors are in parallel. The problem statement says nothing about this, and we could equally likely consider them in series...So what is the point here ?
|
physick
2011-10-16 07:56:18 |
I think what they meant to say in the problem is that BOTH pairs of oppositely charged plates are connected by wires. This would put the capacitors in parallel.
|
Quark
2011-10-19 13:08:52 |
They are not in parallel they are in SERIES. If you read the question it says that they are reconnected "to EACH OTHER with resistive wires such that PLATES (plural) of opposite charge are connected to together". Although the question is not completely straightforward, I would definitely lean towards a series connection by just looking at the context of the problem. There is no indication that the connection is parallel. Especially since they're saying that plates of opposite charge are connected to each other. That means + to - and - to +.
|
|  | highgear
2006-06-07 10:41:25 | Just a simple mistype. Charge is measured in Coulombs as in F=C/V so F*V=C. |  | quantumleap
2006-03-25 11:33:23 | Just for the exercise, let's say capacitors were connected so that the plates of equal sign of charge are connected together (+ connected to +, - to -).
The way I see it, the only correction would be to recalc total charge ?
( Q(total) = 15 in that case ) |  | jax
2005-11-30 06:39:51 | Thanks for your help! |  | yosun
2005-11-26 02:37:27 | jax: i have posted an accompanying figure (above) for this problem. the figure should shed light on the multiple states involved as well as the charge configuration for each state. hope that helps!
ali8
2011-07-28 04:40:12 |
That figure does not exist anymore, could you please reupload it ?
|
|  | jax
2005-11-25 15:36:12 | I don't understand why you subtract the charges immediately after attaching the two capacitors together. Maybe I'm thinking about them being connected wrong?? I was thinking about this sort of configuration...
+- +-
---| | --- | |---
C1 C2
And then I was saying that Q_total = Q1+Q2 =15, and then redistributing the charges and using conservation of charge Q_total = q'1+q'2.
Then I got it wrong and I looked at your solution and I see that you have Q_total = Q1-Q2... why is this? |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
