|
GR9677 #4
|
|
|
|
|
Alternate Solutions |
vorikz
2019-08-21 14:04:36 | I did this in a slightly more simple minded way.\r\n\r\nI knew that oscillation frequency looks something like \r\n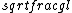 \r\n\r\nwhich is just \r\n\r\nwhich is just 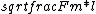 \r\n\r\nThe only solutions with those exact units were A and B, so it was down to a 50/50 guess with 0 work put in. \r\n\r\nThe only solutions with those exact units were A and B, so it was down to a 50/50 guess with 0 work put in. |  | djh101
2014-09-19 21:38:40 | To expand a little bit on the quick and dirty method (point 2, specifically):
1. Small oscillations aren't going to depend on displacement. Eliminate BDE.
2. Experience with small oscillations should tell you that from the potential you are going to get a Hooke's-Law-esgue force, which will give you k. To get the frequency, take the square root of k and divide by the square root of m. Only A has root m in the denominator. |  | archard
2010-05-14 10:06:55 | The way I did it is to remember from freshman physics that the period of an oscillation (and thus the frequency) is independent of displacement. That eliminates B, D and E. A and C are the same save for a square root, so one of them has incorrect dimensions. Choose the one with dimensions of frequency, A. |  | chri5tina
2006-11-27 05:11:24 | It is possible to do this problem w/o the binomial expansion.
Take F = -k*x, plug in -dV/dx for F and solve for k.
Plug k into w = (k/m)^1/2 and you'll have an expression with (R^2 + x^2)^3/2 in the denominator.
At this point you can remember that R >> x and simply cancel out x as negligible, which leaves R^3 in the denominator and the correct solution. |  |
|
|
Comments |
vorikz
2019-08-21 14:04:36 | I did this in a slightly more simple minded way.\r\n\r\nI knew that oscillation frequency looks something like \r\n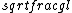 \r\n\r\nwhich is just \r\n\r\nwhich is just 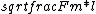 \r\n\r\nThe only solutions with those exact units were A and B, so it was down to a 50/50 guess with 0 work put in. \r\n\r\nThe only solutions with those exact units were A and B, so it was down to a 50/50 guess with 0 work put in. |  | fredluis
2019-08-08 06:55:51 | This is in principle easier because one is dealign with a scalar, and not the electric field which is a vector.tile contractor |  | djh101
2014-09-19 21:38:40 | To expand a little bit on the quick and dirty method (point 2, specifically):
1. Small oscillations aren't going to depend on displacement. Eliminate BDE.
2. Experience with small oscillations should tell you that from the potential you are going to get a Hooke's-Law-esgue force, which will give you k. To get the frequency, take the square root of k and divide by the square root of m. Only A has root m in the denominator. |  | maxdp
2013-09-24 13:55:12 | It seems stiner905's comment hasn't been noted since s/he didn't mark it correctly, so I'll repost it.
"After the binomial expansion, the potential should have a "-" instead of a "+" in the expansion term. However, a minus exists in the force equation because the test charge has charge -q."
In other words, there are two sign errors in the current solution that cancel out. |  | shak
2010-08-13 15:02:04 | The best and easiest way to solve this problem is using Lagrangian equation of motion.. it is one dimensional system.. so small charge -q is moving only along the x-axis.
Lagrangian is
L=E- V (1)
and
E=m*x(dot)^2/2 (2)
V= same potential in problem 3.
|  | archard
2010-05-14 10:06:55 | The way I did it is to remember from freshman physics that the period of an oscillation (and thus the frequency) is independent of displacement. That eliminates B, D and E. A and C are the same save for a square root, so one of them has incorrect dimensions. Choose the one with dimensions of frequency, A.
nkqed
2011-10-24 17:01:10 |
I'm sorry but this is the wrong way to think about it. x is not the displacement. We are displacing the particle perpendicular to x. And if you consider the situation where R is not >> x then we will have some dependence on x.
|
ian
2012-10-05 09:56:53 |
nkqed:
x is the displacement - look at the diagram. Also, the problem only asks us to consider the case where R >> x. I don't see anything wrong with archard's approach.
|
Prufrock
2013-09-16 14:44:53 |
This is a good way to approach it. Barring possible pathological cases, the frequency in a SHO "obviously" doesn't depend on the displacement.
|
|  | Muphrid
2009-10-08 14:06:53 | It may be faster to keep working with electrical potential to find the spring constant. Simple harmonic oscillators satisfy  = -kx) , as has been said, but they also satisfy , as has been said, but they also satisfy
 \approx U_0 + \frac{1}{2} k x^2)
and have angular frequency
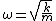
It's important to remember that what you know from problem (3) is ) , potential energy per unit charge, not , potential energy per unit charge, not ) , which is real potential energy. This is what alleviates the sign confusion later on. , which is real potential energy. This is what alleviates the sign confusion later on.
As in the base solution, you can binomial expand ) and approximate it as and approximate it as
 = \frac{Q}{4\pi \epsilon_0} \frac{1}{R} \left( 1 - \frac{1}{2} \frac{x^2}{R^2} \right))
Note that the 1 can be dropped; this just gives a constant overall potential that we're not interested in. This leaves us with
 = V_0 - \frac{1}{2} \frac{Q x^2}{4 \pi \epsilon_0 R^3})
And now multiply through by 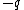 , the charge of the test charge, to get real potential energy: , the charge of the test charge, to get real potential energy:
 = -q V_0 + \frac{1}{2} \frac{qQ x^2}{4 \pi \epsilon_0 R^3})
Recognize this as a simple harmonic potential, where
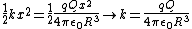
And thus
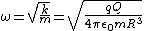 |  | tinytoon
2008-11-07 14:48:10 | Also, you could derive the electric field from first principles to get the answer (although very inefficient). This is, nonetheless, a valid alternative:
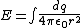
We only care about the horizontal component because the force in the vertical component is zero:
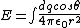 . .
Using 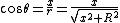 and and 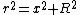 , we get: , we get:
^{3/2}})
and
^{3/2}} =kx)
We can clearly see now that:
^{3/2}}) . .
We know that:
^{3/2}m}})
In the limit that 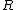 >> >> , this reduces to: , this reduces to:
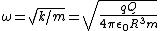 . .
|  | gn0m0n
2008-10-19 17:49:35 | What are we expanding, exactly? |  | dcan
2008-04-09 16:32:33 | Can someone tell me why it doesn't work to use conservation of energy? Supposedly the potential energy is qV, but when I solve for  I'm off by a factor of 1/ I'm off by a factor of 1/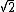 . . |  | Gaffer
2007-10-26 14:12:55 | This problem has some particularly generous writers.
For small oscillations, I believe it is safe to say  must be a constant, that is not dependent upon x. This knocks off BDE. Then all you need to remember is that must be a constant, that is not dependent upon x. This knocks off BDE. Then all you need to remember is that  will most likely involve a square root due to the diffEQ yosun mentioned and you have choice A, no dimensional analysis or calculation necessary. will most likely involve a square root due to the diffEQ yosun mentioned and you have choice A, no dimensional analysis or calculation necessary.
Though of course it is always better to know why a particular formula is correct, sometimes quick and dirty is the way to go.
Oh that they were all this easy!
jmason86
2009-09-29 16:40:35 |
This is exactly how I did the problem too. Definitely the right strategy under time pressure.
|
|  | rmyers
2006-11-29 16:16:57 | This can also be done just by dimensional analysis. Qq/(4pi(e0)R^2) has units of force = kg * m/s^2 and angular frequency is just 1/s. Only A & B are possible answers after this. From there I suppose you can just use the idea that the angular frequency usually doesn't depend on initial displacement in cases like these.
eliasds
2008-08-18 00:58:43 |
I believe that choice E has the same dimensions as A&B.
|
eliasds
2008-08-18 01:43:44 |
I believe that choice E has the same dimensions as A&B.
|
wangjj0120
2008-10-11 01:12:02 |
rmyers:
your comment "you can just use the idea that the angular frequency usually doesn't depend on initial displacement" is not always true. You can find the x dependence from the exact solution.
|
|  | chri5tina
2006-11-27 05:11:24 | It is possible to do this problem w/o the binomial expansion.
Take F = -k*x, plug in -dV/dx for F and solve for k.
Plug k into w = (k/m)^1/2 and you'll have an expression with (R^2 + x^2)^3/2 in the denominator.
At this point you can remember that R >> x and simply cancel out x as negligible, which leaves R^3 in the denominator and the correct solution. |  | stiner905
2006-10-29 12:26:06 | After the binomial expansion, the potential should have a "-" instead of a "+" in the expansion term. However, a minus exists in the force equation because the test charge has charge -q. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
