|
GR9677 #26
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
wittensdog
2009-10-30 13:47:27 | I'm noticing that in a lot of cases, you can make some pretty liberal approximations and still be okay for the GRE. In this problem, if you say pi^2 = 10 , and that the broadcast frequency is 100 MHz and not 103.7 MHz, the math becomes amazingly faster. Now, with approximations like that, we're certainly adding some small errors, but in the case of the frequency it's in the third significant digit, and the difference between pi^2 and 10 in reality is only about 0.13. Now, the answer you get with this method is (1/8) * 10 ^ -11, which works out to be 1.25 * 10 ^ -12, or about a picoFarad. Without even knowing the decimal value of 1/8, you can see that we're on the order of 10 ^ -12. So we're probably looking at choice C.
The next closest choice is D, but that's a factor of 5 lower. Now, we may not know exactly how good our approximations are, but we're definitely not talking about factors of 5 in error here. And going the other way to choice B would be an error factor of 50!
So forget the extra significant digits, there's no point in getting your results to that kind of accuracy when the answer choices are so widely spaced out. The extreme case occurs when the answer choices are separated by like factors of 1000, then don't even bother with the factors at all, just look at powers of ten and shoot for the right ballpark.
Sometimes even when I've been trying to discriminate between two close choices, I've noticed that just paying attention to whether my approximation is shooting me too high or too low will let me get to the right answer.
So, despite my long rambling, my point is, I don't think the math in this problem is hard at all, so long as you toss out accuracy you don't need. |  | chemicalsoul
2009-10-17 01:31:46 | w^2=(1/LC)-(R/2L)^2
Using this formula, I got ans approx equal to 0.5*10^-11.
Prologue
2009-10-20 12:44:18 |
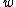 is not equal to 103.7 MHz, is not equal to 103.7 MHz, 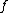 is. And using is. And using 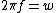 you see that you need to multiply 103.7 MHz by you see that you need to multiply 103.7 MHz by 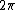 to get omega. to get omega.
|
anum
2010-11-08 09:07:23 |
that's the mistake i did.
|
RusFortunat
2015-10-20 14:07:36 |
not just you
|
|  | Walter
2009-01-05 15:34:46 | The resonant frequency of an LRC-circuit depends on R, in fact
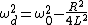
where  is the resonant frequency of the undamped LC circuit, so before grinding out an answer you would need to check that is the resonant frequency of the undamped LC circuit, so before grinding out an answer you would need to check that  which you can do as for all the possible answers the magnitude of which you can do as for all the possible answers the magnitude of 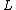 is such that the prior condition applies and thus is such that the prior condition applies and thus 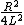 can be neglected. can be neglected.
It's a bit gung-ho given how mean some questions are to just ignore the resistance.
wittensdog
2009-10-16 19:37:45 |
This is indeed the natural oscillation frequency of an RLC circuit, but you still don't need to consider the resistance, for the following reason.
The condition that,
1/w = sqrt(LC)
actually comes from considering the impedance of an RLC circuit. For a given resistance, the largest possible power is dissipated across the circuit when the imaginary portion of the impedance, or the reactance, is zero. So if we specify that we are using a given resistance in the circuit, then the condition for maximum power absorption comes from setting the imaginary portion of the impedance to zero. It turns out that resistors have a purely real resistance, and capacitors and inductors have purely imaginary impedance. So we need to have the sum of the reactances of the capacitor and inductor be zero. Because these reactances are frequency dependent, this then becomes a condition that involves the frequency, inductance, and capacitance, but not the resistance.
|
syreen
2013-09-11 15:42:22 |
so, is there a QUICK way to tell whether or not R can be neglected?
|
maxdp
2013-09-24 22:04:50 |
Yup. Pretty sure as long as the circuit is hooked up to a power source (as a radio must be), then the power basically "pushes through" the resistor and gives the 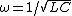 that most people in this thread are using. And for the GREs, it seems unlikely that they'd expect you to remember the full formula for the frequency when a power source is not connected (called the damped frequency), which is what Walter is talking about. that most people in this thread are using. And for the GREs, it seems unlikely that they'd expect you to remember the full formula for the frequency when a power source is not connected (called the damped frequency), which is what Walter is talking about.
|
|  | gumpstuck
2008-09-22 21:39:47 | Just to clarify and sum up previous comments:
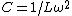
here 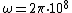
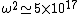
so we have, (5\times10^{17})}=10^{-12}) which is choice (C). which is choice (C). |  | gatboja
2005-12-08 12:27:08 | yosun, i believe you missed a squared sign for the 100E6. |  | StudyTime
2005-11-10 20:56:18 | Mexicorn, you missed that you need to multiply the broadcast frequency by 2*pi to get the angular freqency. |  | Mexicorn
2005-11-10 17:20:49 | woops, those x's should be multiplications and that -13 should be a positive at the in the last fraction I wrote |  | Mexicorn
2005-11-10 17:18:34 | I'm not sure if i'm doing some math weird, but I can't understand how you got choice C for the problem. Using 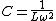 I end up with I end up with (1.03x10^{8})^{2}}) which gives me which gives me 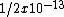 or (D). Isn't the frequency supposed to be squared? Or am I missing something trivial? or (D). Isn't the frequency supposed to be squared? Or am I missing something trivial?
sabinscabin
2008-10-04 14:51:09 |
you're squaring the frequency, not omega. it's not 1.03e8^2, but (2pi * 1.03e8)^2
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
