|
GR9677 #15
|
|
|
Problem
|
|
|
This problem is still being typed. |
Thermodynamics }Phase Diagram }Phase Diagram
Recall that for an ideal gas 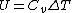 and and  . Don't forget the first law of thermodynamics, . Don't forget the first law of thermodynamics, 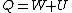 . .
For  , , 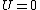 , since the temperature is constant. Thus, , since the temperature is constant. Thus, 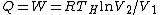 . .
For 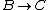 , , 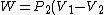=R(T_c-T_h)) . . 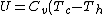) , and thus , and thus 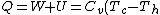-R(T_h-T_c)) . .
For 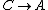 , , 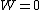 , , 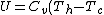) , thus , thus 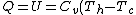) . .
Add up all the Q's from above, cancel the 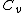 term, to get term, to get -R(T_h-T_c)) , as in choice (E).s , as in choice (E).s
|
|
|
Alternate Solutions |
ssp
2008-09-08 03:26:43 | 3-step cycle with isovolumetric part that has W = 0, so we need an added heat for two steps (read two parts). That already eliminates (A) through (C). Then for the last part just dimensional analysis... (D) does not work cause we are missing a mass to convert the 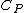 to joules.... that only leaves (E) to joules.... that only leaves (E) |  |
|
|
Comments |
nirav_605
2013-10-16 12:44:43 | In Process from B to C
Isn't that suppose to be C_p not C_v
The process occurs at constant pressure not volume.
Giuseppe
2015-09-11 15:04:33 |
For the isobar B-C you have to use C_p for the heat absorbed (Q) and C_v for the change in internal energy (U), since the change in internal energy in B-C has to be equal and opposite to that of C-A.\r\nInfact, for BC:\r\nQ = -Cp(Th-Tl)\r\nU = -Cv(Th-Tl)\r\nW= -P(V2-V1)\r\nwhich also gives P(V2-V1) = R (Th-Tl)
|
|  | mvgnzls
2011-09-07 18:01:05 | why is there no n in the formulas?
pv=(n)RT & W= -nRTln(vf/vi)
why do the n's get left out?
pam d
2011-09-11 18:41:05 |
n = 1, so you are right in looking for it but make sure you read the question very carefully
|
|  | jmason86
2009-09-30 17:22:25 | I also realized that 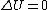 therefore Q=W which is the area in the curve. However, the way I actually solved the problem was to look at the answers. (D) and (E) both had a first term that I knew was an isothermal work term. Also, the two answers were essentially identical, so the correct answer was probably one of those. therefore Q=W which is the area in the curve. However, the way I actually solved the problem was to look at the answers. (D) and (E) both had a first term that I knew was an isothermal work term. Also, the two answers were essentially identical, so the correct answer was probably one of those.
Looking at the 2nd terms, they obviously had different units. The units in the 2nd term of (D) are not consistent with the units in its first term.. you can't even do this subtraction. Eliminate (D). (E) remains.
noether
2009-11-03 21:04:57 |
Answer D does have correct units, see the responses to ssp's solution.
|
|  | mudder
2009-09-28 02:13:31 | An alternate way of looking at this is
Work = area of PV diagram
Since delta-U = o, then Q = area of PV diagram
Find the equation of the T_h isotherm using the ideal gas law, and integrate the PV region to find the area. That area is the added heat. |  | duckduck_85
2008-11-06 16:43:43 | radicaltyro's is the best and quickest solution |  | ssp
2008-09-08 03:26:43 | 3-step cycle with isovolumetric part that has W = 0, so we need an added heat for two steps (read two parts). That already eliminates (A) through (C). Then for the last part just dimensional analysis... (D) does not work cause we are missing a mass to convert the 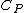 to joules.... that only leaves (E) to joules.... that only leaves (E)
Walter
2009-01-01 08:57:19 |
Rejecting (D) on the grounds that we are "missing a mass" is not justified. The questions specifies that 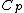 is a molar heat capacity and also that there is one mole of gas hence any is a molar heat capacity and also that there is one mole of gas hence any 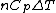 term in the result would simplify to term in the result would simplify to  . Hence you remain stuck with a 50/50. . Hence you remain stuck with a 50/50.
radicaltyro's solution is best.
|
okdisa
2009-09-22 18:23:41 |
Actually, 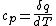 so so ) does in fact have the correct units. Don't forget that heat and energy are equivalent dimensionally. does in fact have the correct units. Don't forget that heat and energy are equivalent dimensionally.
|
Giuseppe
2015-09-11 15:08:42 |
You can\'t use dimensional analysis to eliminate choice D, it has the correct units. Cp is heat capacity at constant pressure per mole, and there is a factor of 1mole implicitaly multiplied everywhere in the solutions.
|
|  | kyros
2007-11-01 11:27:59 | Shouldn't the B->C term have a C_p not a C_v?
Imperate
2008-09-04 09:38:50 |
Yes.
B->C:
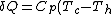=-C_p (T_h-T_c) )
C->A:
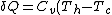 )
Adding contributions from these parts, one obtains:
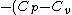(T_h-T_c) )
and remembering that for an ideal gas 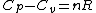 provides(setting n=1mole): provides(setting n=1mole):
 ) , which is the last term. , which is the last term.
|
|  | radicaltyro
2006-11-02 17:21:59 | You don't need to calculate 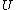 for each step. Just note that this is a cyclic process so for each step. Just note that this is a cyclic process so 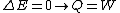 and add up the and add up the 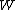 's. 's.
newton
2007-09-29 06:35:00 |
cool solution
|
prismofmoonlight
2007-11-01 23:30:12 |
agreed.
|
tonyhong
2008-10-04 04:24:55 |
so there is nothing to do with Cp and Cv, answers B,C,D excluded. A is excluded for simple reason
|
wittensdog
2009-10-16 15:23:50 |
Indeed, I think I was almost implicitly doing this without even really thinking about it, but it's definitely a good general principle to remember.
The same idea applies for entropy, or any other state variable. As long as we're working with a constant amount of stuff, then things like pressure, volume, entropy, internal energy, and temperature are all specified when you choose a point on the PV diagram. So as long as you move around a closed loop, when you come back to the original point, then you end up with the same value as before. So indeed, when you go around the cycle, since you come back to the same point, you must have the same internal energy as before. This means that the heat added over the course of the cycle (eventually) all went into doing work. Of course this wouldn't be true in general if you just looked at a portion of the plot (though it is true for isotherms of ideal gases).
|
|  | beibei
2006-06-14 12:40:26 | Why I can not see the problems of 9677 15,16...only the solutions. some of the questions have this problem
godkun1
2017-03-15 17:29:41 |
You are right
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
