zwarner0891
2017-08-25 14:23:44 | Here is an approach that requires little to know knowledge of atomic physics. The nucleus shouldn\'t emit anything since it is no longer excited after giving its energy to the electron so C,D,E are out. Why should the Atom be around other atoms? Who says it can not be alone? A is out. This only leaves B which is the right answer! I could be wrong in my thinking so let me know. \r\n |  |
saar
2014-04-01 01:28:59 | This situation leads to Auger electron or X-ray. While refer to "http://en.wikipedia.org/wiki/Auger_electron_spectroscopy" (Figure 4), it's quite clear that for high atomic number x-ray yield is crucial.
Also Auger electron has nothing to do with the nucleus |  |
asdfhey
2011-05-19 17:10:24 | Even though the emission of an Auger electron is possible, it is impossible that the "nucleus emits it." |  |
Kabuto Yakushi
2010-09-05 09:56:05 | One can get the answer without any knowledge of internal conversion. (C), (D), and (E) are all products of radioactive decay which are results of unstable nuclei. The problem tells us that after internal conversion the atom (not the nucleus) is in an exited state leaving it up to the electrons to return the atom to ground state. This leaves just (B). (A) is just plain silly.
aprilrussell
2018-05-30 03:50:43 |
This seems the best solution. Yosun\'s is rather ambiguous. run 3
|
|  |
shak
2010-08-14 08:57:39 | Most internal conversion electrons come from the K shell (1s state, see electron shell), as these two electrons have the highest probability of being found inside the nucleus. After the electron has been emitted, the atom is left with a vacancy in one of the inner electron shells. This hole will be filled with an electron from one of the higher shells and subsequently a characteristic x-ray or Auger electron will be emitted.
Ge Yang
2010-10-07 09:46:46 |
This seems the best solution. Yosun's is rather ambiguous.
|
|  |
kolahalb
2007-11-11 07:02:21 | What comes to my mind is that mentioning "high atomic number" leads us to a definite conclusion that there exist other shells,say L,M,N...from which electron transition might occur.
If the atom happened to have very low atomic number,this would not be possible.
student2008
2008-10-17 05:34:59 |
"High atomic number" tells us that 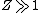 , so even for K-series , so even for K-series ^2\gg Ry) , thus it's not optical but X-ray radiation. , thus it's not optical but X-ray radiation.
|
|  |
prismofmoonlight
2007-11-01 23:10:52 | Why do they (ETS) point out that the atom has a high atomic number? (i.e. "The most probable process after an internal conversion electron is ejected from an atom with a high atomic number is...") Does it have significance?
zaijings
2009-04-01 20:00:26 |
for low atomic number, it will produce the auger effect and ionize the outside electron. for high atomic number, only thing it can do is emit X rays.
|
|  |
sharpstones
2007-04-02 19:56:01 | When an inner electron is ejected, the atom is left in an excited state. Jumping to a lower energy state one of the outer electrons will drop down to fill the hole. This transition will have its corresponding emitted photon which occurs whenever an electron makes a transition between energy levels in an atom.
From this point just remember:
electron transitions (in atom) = X-ray production
nuclear transitions = Gamma Ray production |  |
