|
GR9277 #84
|
|
|
Problem
|
|
\prob{84}
An electron oscillates back and forth along the + and -x axes, consequently emitting electromagnetic radiation. Which of the following statements concerning the radiation is NOT true?
- The total rate of radiation of energy into all directions is proportional to the square of the electron's acceleration.
- The total rate of radiation of energy into all directions is proportional to the square of the electron's charge.
- Far from the electron, the rate at which radiated energy crosses a perpendicular unit area decreases as the inverse square of the distance from the electron
- Far from the electron, the rate at which radiated energy crosses a perpendicular unit area is a maximum when the unit area is located on the + or - x-axes
- Far from the electron, the radiated energy is carried equally by the transverse electric and the transverse magnetic fields.
|
Electromagnetism }Accelerating Charges }Accelerating Charges
Elimination time:
(A) By the Larmor formula, one has 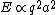 , where q is the charge and a is the acceleration. Since the charge is constant, this choice is true. , where q is the charge and a is the acceleration. Since the charge is constant, this choice is true.
(B) This is also true by Larmor's formula.
(C) True. The energy radiated through a perpendicular unit area is given by the Poynting vector.  \propto E^2\hat{r}-(\hat{r}\cdot\vec{E})\vec{E}) and and 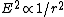 far away. Also, less rigorously, one can arrive at the same result from recalling the surface area of a sphere, far away. Also, less rigorously, one can arrive at the same result from recalling the surface area of a sphere, 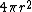 , and thus any term in , and thus any term in  proportional to proportional to 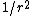 will yield a finite, thus acceptable answer. (Thanks to the user astro_allison for this pointer. See p460ff of Griffiths, Introduction to Electrodynamics, 3rd Edition for more details.) will yield a finite, thus acceptable answer. (Thanks to the user astro_allison for this pointer. See p460ff of Griffiths, Introduction to Electrodynamics, 3rd Edition for more details.)
(D) False. It's a minimum in the plane.
(E) True, since far from the electron the field behaves as plane waves, with 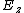 and and 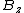 both 0. both 0.
|
|
|
Alternate Solutions |
Herminso
2009-09-22 14:16:29 | Remember the Larmor Formula 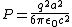 , thus (A) and (B) are right. , thus (A) and (B) are right.
Now, for a electric dipole =qd\cos {(\omega t)}\hat{x}) we have: we have:
![\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}](/cgi-bin/mimetex.cgi?\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}) and and ![\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\phi}](/cgi-bin/mimetex.cgi?\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\phi})
You see then that far from the electron, the radiated energy is carried equally by the transverse electric and the transverse magnetic fields.Then (E) is true.
To see if the rate at which radiated energy crosses a perpendicular unit area decreases as the inverse square of the distance from the electron, look for the Pointing vector:
\frac{\sin^2 {\phi}}{r^2}\hat{r}) , thus (C) is also true. , thus (C) is also true.
But (D) is false if from the expresion above for the electric field you can see that it ahve a minimum at 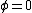 , just the x-axes. , just the x-axes.
|  |
|
|
Comments |
tn
2018-01-23 02:39:21 | If, 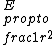 and and  , then wouldn\'t , then wouldn\'t 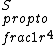 ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field 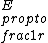 . Then we can conclude . Then we can conclude 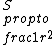 . .
tn
2018-01-23 02:43:54 |
TYPO! comment above should read:\r\n\r\nIf, 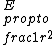 and and  , then wouldn\'t , then wouldn\'t 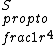 ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field 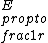 . Then we can conclude . Then we can conclude 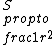 . .
|
tn
2018-01-23 02:46:39 |
TYPO! comment above should read:\r\n\r\nIf, 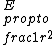 and and  , then wouldn\'t , then wouldn\'t 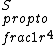 ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field ? I think the answer to this problem is contingent upon being able to model the oscillating electron as a Hertzian dipole, which generates a field 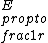 . Then we can conclude . Then we can conclude 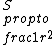 . .
|
|  | Herminso
2009-09-22 14:16:29 | Remember the Larmor Formula 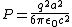 , thus (A) and (B) are right. , thus (A) and (B) are right.
Now, for a electric dipole =qd\cos {(\omega t)}\hat{x}) we have: we have:
![\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}](/cgi-bin/mimetex.cgi?\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}) and and ![\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\phi}](/cgi-bin/mimetex.cgi?\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\phi}}{r})\cos {[\omega(t-r/c)]}\hat{\phi})
You see then that far from the electron, the radiated energy is carried equally by the transverse electric and the transverse magnetic fields.Then (E) is true.
To see if the rate at which radiated energy crosses a perpendicular unit area decreases as the inverse square of the distance from the electron, look for the Pointing vector:
\frac{\sin^2 {\phi}}{r^2}\hat{r}) , thus (C) is also true. , thus (C) is also true.
But (D) is false if from the expresion above for the electric field you can see that it ahve a minimum at 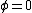 , just the x-axes. , just the x-axes.
|  | georgi
2007-08-27 00:10:23 | i'm not sure i understand why d is false. What plane are we talking about? and why is that true?
a19grey2
2008-11-02 14:33:05 |
Yosun is referring to the Y-Z plane in this problem. The maximum amount of energy radiated is along the x-axis (the axis of acceleration) and it is minimum perpendicular to the axis of acceleration).
|
Crandor
2010-04-08 19:13:17 |
Exactly backwards, a19grey2. Power radiated is minimum (0) along the axis of motion and maximum along the plane perpendicular to that axis.
|
|  | astro_allison
2005-11-26 04:52:46 | (c) is true because energy (radiated energy here) is proportional to the inverse square of the distance. I know this is more or less exactly what the problem states; just remember that for and electron, 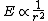 , where r is the distance. , where r is the distance.
Andresito
2006-03-29 15:09:21 |
@ astro_allison, thank you for the reference.
@ Yosun, correct page is "460"
|
|  | astro_allison
2005-11-26 04:15:07 | 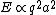
astro_allison
2005-11-26 04:15:37 |
(from griffiths em)
|
yosun
2005-11-26 18:14:17 |
astro_allison: thanks for the typo-alert regarding Larmor's formula, as well as the pointer to check Griffiths.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
