|
GR9277 #81
|
|
|
|
|
Alternate Solutions |
student2008
2008-10-16 10:47:38 | We need to distinguish between the resonance of currents and that of other quantities (voltage, charge, etc.). The simplest way here is to write the equation for current in the complex form:
I_m e^{i(\omega t +\delta)}=\epsilon_m e^{i\omega t}) , where , where 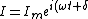}) , , 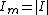 . .
Thus, 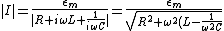^2}}) . Since the sum of the squares is the smallest when the second square is equal to zero, we obtain (C). . Since the sum of the squares is the smallest when the second square is equal to zero, we obtain (C).
To the contrary, if we want, for example, to achieve the maximum voltage on the capacitor, or the maximum emf of the coil, we need to integrate or differentiate the expression for the current given above with respect to  , and then take derivatives of modules of that expressions with respect ot , and then take derivatives of modules of that expressions with respect ot  . Thus, the frequency would be someway shifted, as in choice (D). . Thus, the frequency would be someway shifted, as in choice (D). |  |
|
|
Comments |
neon37
2010-11-12 06:29:46 | Here we have a RLC driven circuit. And we are trying to find frequency, so isnt it the one that doesnt have R dependance? |  | student2008
2008-10-16 10:47:38 | We need to distinguish between the resonance of currents and that of other quantities (voltage, charge, etc.). The simplest way here is to write the equation for current in the complex form:
I_m e^{i(\omega t +\delta)}=\epsilon_m e^{i\omega t}) , where , where 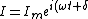}) , , 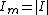 . .
Thus, 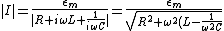^2}}) . Since the sum of the squares is the smallest when the second square is equal to zero, we obtain (C). . Since the sum of the squares is the smallest when the second square is equal to zero, we obtain (C).
To the contrary, if we want, for example, to achieve the maximum voltage on the capacitor, or the maximum emf of the coil, we need to integrate or differentiate the expression for the current given above with respect to  , and then take derivatives of modules of that expressions with respect ot , and then take derivatives of modules of that expressions with respect ot  . Thus, the frequency would be someway shifted, as in choice (D). . Thus, the frequency would be someway shifted, as in choice (D). |  | DaveyClaus
2006-11-28 19:36:09 | I guess ETS likes  solutions! Am I wrong or is D the actual solution for unspecified R, L, and C? solutions! Am I wrong or is D the actual solution for unspecified R, L, and C?
freeform
2006-11-28 20:49:26 |
Now I think I get this problem. Answer D is for underdamped circuit (R small) ONLY if the voltage source is a DC switched on (to charge capacitor) and then off--behavior is an exponentially decaying sinusoid.
Here we have a continuously driving AC source, so the voltage should look just like a pure LC circuit (sinusoidal). Remember LRC circuits in electronics lab?
|
pam d
2011-09-30 17:27:26 |
This discussion is exactly why it is important they noted that the transients have died out. The general solution of a driven oscillator differential equation contains two parts, first is the solution to the homogeneous diffeq (in other words your LRC circuit without a driving voltage source) that is dependent upon initial conditions. This is the transient part because it dies off exponentially.
The second part of the general solution is independent of initial conditions and is purely oscillatory. This is called the "steady state" solution because if you wait long enough (long enough for the transient part to decay away) you are going to end up with it alone. The steady state angular frequency for maximum current amplitude is (C) for reasons discussed by yosun and jax six years ago below.
|
|  | jax
2005-12-06 13:59:54 | Isn't the impedance 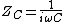 and and 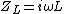 , and then resonance occurs when , and then resonance occurs when 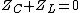 so Z_C = -Z_L so Z_C = -Z_L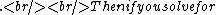 \omega \omega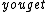 \omega = \sqrt{\frac{1}{LC}}$ \omega = \sqrt{\frac{1}{LC}}$
I'm not sure if there is some case when you can do this the way it was done above without complex impedances, but this is the way I learned it.
jax
2005-12-06 14:00:41 |
Isn't the impedance 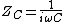 and and 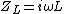 , and then resonance occurs when , and then resonance occurs when 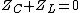 so so  . .
Then if you solve for  you get you get 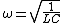
I'm not sure if there is some case when you can do this the way it was done above without complex impedances, but this is the way I learned it.
|
yosun
2005-12-06 19:44:48 |
jax: actually, I believe impedance is given by the modulus of | =\sqrt{R^2+(X_c-X_L)^2}) , and resonance occurs when , and resonance occurs when 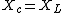 for a minimal impedance. The for a minimal impedance. The 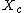 and and 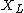 don't involve the imaginary term, per se. don't involve the imaginary term, per se.
|
jax
2005-12-06 21:31:32 |
I guess that condition (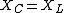 ) holds for resonance, but you're setting the reactance (X) equal, not the impedance (Z). ) holds for resonance, but you're setting the reactance (X) equal, not the impedance (Z).
If you want the condition for resonance in terms of impedance (Z) see my previous post.
I'm just getting all confused with reactance vs. impedance now! These websites are useful...
http://en.wikipedia.org/wiki/Reactance />
http://en.wikipedia.org/wiki/Impedance />
http://en.wikipedia.org/wiki/RLC_circuit
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
