GREPhysics.NET: GR9277 #77

GR9277 #77

Problem

GREPhysics.NET Official Solution

\prob{77}
Consider a heavy nucleus with spin 1/2. The magnitude of the ratio of the intrinsic magnetic moment of this nucleus to that of an electron is

zero, because the nucleus has no intrinsic magnetic moment
greater than 1, because the nucleus contains many protons
greater than 1, because the nucleus is so much larger in diamter than the electron
less than 1, because of the strong interactions among the nucleons in a nucleus
less than 1, because the nucleus has a mass much larger than that of the electron

Quantum Mechanics $\Rightarrow$ }Gyromagnetic Ratio

The intrinsic magnetic moment is defined in terms of the gyromagnetic ratio and spin as $\vec{\mu}_s = \gamma \vec{S}$ , where $\gamma = \frac{eg}{2m}$ (g is the Lande g-factor).

Thus, one sees that the magnetic moment is inversely related to mass.

The ratio of the magnetic moment of a nucleus to that of an electron is $\mu_n/\mu_e = m_e/m_n << 1$ , as in choice (E). (One can cancel out the S since ETS is nice enough to have the nucleus have the same spin as the electron.).

Alternate Solutions

Ning Bao
2008-01-30 07:26:00

a common sense answer: presumably the more magnetically "efficient" (e.g. gets the same result for less material, or mass) thing would have a higher intrinsic magnetic moment. Bang for the buck theory wins again.

Reply to this comment

Comments

Ning Bao
2008-01-30 07:26:00

Reply to this comment

rmyers
2006-12-01 13:05:25

Presumably the nucleus would also have a larger charge so the top term would increase as well. However the charge would only end up being a hundred times larger at most, while the mass is many orders of magnitude larger than an electron.

student2008
2008-10-16 08:15:53

You're right! Also, g-factors of electron, proton and neutron differ (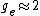 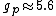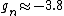$g_e\approx 2$ , $g_p\approx 5.6$ , $g_n\approx -3.8$ ). But this is not relevant for the ratio, for the same reason.

Reply to this comment

Post A Comment!

You are replying to:

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

<a href="http://www6.shoutmix.com/?grephysics">View shoutbox</a>
ShoutMix chat widget

Free 3D Virtual World. Largest User-Created Fantasy World. Don't Play, Experience. Join Now!

Bored, got time to kill, and want to earn micro-cash by mindlessly clicking on links? Join CrownGPT. Click Offers. Click the Paid to Click button... then click to your heart's delight.

FREE 3D Virtual World Chat - Join Second Life Today!

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone