|
GR9277 #76
|
|
|
|
|
Alternate Solutions |
Mall-Saint
2016-10-23 00:32:38 | We have l=0+1+1=2. Each electron has s=1/2. If we have two electrons, the possible values of s are 0 and 1. Therefore for three electrons, the possible values of s are 1/2 and 3/2. Hence if we have (l=2, s=1/2) the possible j values are 3/2 and 5/2. But if we have (l=2, s=3/2) the possible j values are 1/2, 3/2, 5/2, 7/2. Hence the largest possible j is 7/2.\r\n\r\nAlso note l=2 because m_l = 0 for the 1s state, but m_l = {-1,0,1} for the 2p and 3p states, and so the total m_l can take any value from {-2,-1,0,1,2} -> l=2. |  |
|
|
Comments |
Mall-Saint
2016-10-23 00:32:38 | We have l=0+1+1=2. Each electron has s=1/2. If we have two electrons, the possible values of s are 0 and 1. Therefore for three electrons, the possible values of s are 1/2 and 3/2. Hence if we have (l=2, s=1/2) the possible j values are 3/2 and 5/2. But if we have (l=2, s=3/2) the possible j values are 1/2, 3/2, 5/2, 7/2. Hence the largest possible j is 7/2.\r\n\r\nAlso note l=2 because m_l = 0 for the 1s state, but m_l = {-1,0,1} for the 2p and 3p states, and so the total m_l can take any value from {-2,-1,0,1,2} -> l=2. |  | jeffray
2011-11-07 11:19:56 | If the state were instead 1s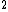 2s3s, would the calculation change to 0 + 1 + 1 + 1/2 - 1/2 + 1/2 + 1/2? Do the two spins cancel out or do we just add another 1/2? 2s3s, would the calculation change to 0 + 1 + 1 + 1/2 - 1/2 + 1/2 + 1/2? Do the two spins cancel out or do we just add another 1/2? |  | ashowmega
2010-04-02 13:01:05 | So, here the electrons are 1s 2p 3p. We know that for s, l=0, for 2p l=-1,0,1, for 3p l=-1,0,1. Hence we have seven values of quantum numbers. And each of them have 1/2 spin angular momentum. Hence, for seven azimutal quantum numbers, the total angular momentum = 7x(1/2) = 7/2 .
I guess what I am thinking is right.
flyboy621
2010-10-22 17:23:43 |
That's not right.
For s states, l=0. For p states, l=1. For spin 1/2 particles (i.e. electrons), s=1/2,m_s=1/2, -1/2.
For this problem we are not concerned with any of the m values, only l and s. We have 6 angular momentum quantities to add together:
0, 1, 1, 1/2, 1/2, 1/2
The outcome of adding these together can be any non-negative number you can get by adding or subtracting them. The maximum possible outcome is when they all add together (instead of subtracting). That gives 7/2, which is the answer. Other possible outcomes are 3, 5/2, 2, 3/2, 1, and 1/2. Zero is not possible.
|
|  | coke_man
2008-08-01 12:56:40 | I know this is a stupid question, but how is the total orbital angular momentum equal to 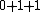 . If there is one electron in the . If there is one electron in the 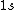 and one in the and one in the 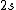 and one in the and one in the 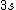 shouldn't the total angular momentum be shouldn't the total angular momentum be 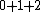 ? Could someone please tell me what I'm missing!!! ? Could someone please tell me what I'm missing!!!
coke_man
2008-08-01 13:01:11 |
Sorry, this should have been categorized under HELP :D
|
note
2008-08-23 16:17:19 |
the s subshell refers to quantum angular momentum number l=0
the p subshell refers to quantum angular momentum number l=1
one electron is in s and two are in p, thus 0+1+1
|
ebykl
2008-10-25 10:18:03 |
What I can't understand is how can 3electrons can go to third shell. 1s^2 2s^2 2p^6......so the 3electrons must be at must at the 2S shell?
|
segfault
2009-09-06 07:43:35 |
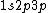 is just a given state. It doesn't necessarily have to be the ground state, is just a given state. It doesn't necessarily have to be the ground state, 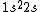
|
Moush
2010-09-28 18:58:26 |
I had the same problem as coke_man, and a lot of others did too (only 25% answered correctly) so this is worth mentioning.
Whenever I saw 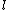 =1, 2, 3, ... n-1, I incorrectly thought =1, 2, 3, ... n-1, I incorrectly thought 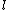 HAS TO BE n-1, but instead HAS TO BE n-1, but instead 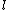 can be UP TO n-1. For some reason I never understood that an e- in orbital s has can be UP TO n-1. For some reason I never understood that an e- in orbital s has 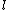 =0, and =0, and 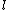 =1 for e- in orbital p, etc., REGARDLESS of the principal quantum number shell it's in. All examples I've seen use PQN + orbital combinations that give the same answer with both correct and incorrect assumptions...until ETS. =1 for e- in orbital p, etc., REGARDLESS of the principal quantum number shell it's in. All examples I've seen use PQN + orbital combinations that give the same answer with both correct and incorrect assumptions...until ETS.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydcol.html#c2
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
