GREPhysics.NET: GR9277 #77

GR9277 #77

Problem

GREPhysics.NET Official Solution

\prob{77}
Consider a heavy nucleus with spin 1/2. The magnitude of the ratio of the intrinsic magnetic moment of this nucleus to that of an electron is

zero, because the nucleus has no intrinsic magnetic moment
greater than 1, because the nucleus contains many protons
greater than 1, because the nucleus is so much larger in diamter than the electron
less than 1, because of the strong interactions among the nucleons in a nucleus
less than 1, because the nucleus has a mass much larger than that of the electron

Quantum Mechanics $\Rightarrow$ }Gyromagnetic Ratio

The intrinsic magnetic moment is defined in terms of the gyromagnetic ratio and spin as $\vec{\mu}_s = \gamma \vec{S}$ , where $\gamma = \frac{eg}{2m}$ (g is the Lande g-factor).

Thus, one sees that the magnetic moment is inversely related to mass.

The ratio of the magnetic moment of a nucleus to that of an electron is $\mu_n/\mu_e = m_e/m_n << 1$ , as in choice (E). (One can cancel out the S since ETS is nice enough to have the nucleus have the same spin as the electron.).

Alternate Solutions

Ning Bao
2008-01-30 07:26:00

a common sense answer: presumably the more magnetically "efficient" (e.g. gets the same result for less material, or mass) thing would have a higher intrinsic magnetic moment. Bang for the buck theory wins again.

Reply to this comment

Comments

alemsalem
2010-09-26 03:52:11

to see how bigger mass results in a smaller magnetic moment (classically) think of it this way:
for a given (spin) angular momentum, the one with the higher mass will have a smaller angular frequency therefore smaller current which means less magnetic moment.
this isn't a complete explanation, but it's good to have a feeling for where the mass came from.

Reply to this comment

Ning Bao
2008-01-30 07:26:00

his dudeness
2010-09-05 07:02:29

I think this kind of reasoning could potentially get you into trouble. For example, I could say "magnetic moment, in classsical terms, is generally current times area. since a nucleus has a much larger "area" than an electron, it should have a larger magnetic moment!" which is clearly wrong.

A better way to think about this problem is to realize that particle magnetic moments are generally proportional to angular momentum, with the constant of proportionality being the "gyromagnetic ratio" (charge over mass). Since nuclei and electrons have the same charge and spin angular momentum, the only difference will be in the masses, so an electron's magnetic moment will be ~2000 times bigger.

Reply to this comment

rmyers
2006-12-01 13:05:25

Presumably the nucleus would also have a larger charge so the top term would increase as well. However the charge would only end up being a hundred times larger at most, while the mass is many orders of magnitude larger than an electron.

student2008
2008-10-16 08:15:53

You're right! Also, g-factors of electron, proton and neutron differ ( 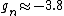$g_e\approx 2$ , $g_p\approx 5.6$ , $g_n\approx -3.8$ ). But this is not relevant for the ratio, for the same reason.

NoPhysicist3
2017-03-23 13:24:06

best remark!

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone