|
GR9277 #74
|
|
|
Problem
|
|
\prob{74}
Two circular hoops, X and Y, are hanging on nails in a wall. The mass of X is four times that of Y, and the diamter of X is also four times that of Y. If the period of small oscillations of X is T, the period of small oscillations of Y is
- T
- T/2
- T/4
- T/8
- T/16
|
Mechanics }Small Oscillations }Small Oscillations
The small oscillations of the hoop has the same frequency as that of a simple pendulum. Thus, 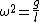 . However, in this case, . However, in this case, 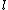 is the distance from the center of mass to the oscillation point---which is just the radius of the loop. is the distance from the center of mass to the oscillation point---which is just the radius of the loop.
Since 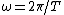 , the period , the period 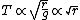 does not depend on mass. does not depend on mass.
Since 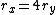 . The ratio of periods is . The ratio of periods is 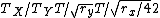 . Thus, the period of Y is just . Thus, the period of Y is just 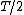 . (Note, the technique of leaving out constants requires that . (Note, the technique of leaving out constants requires that  's are used instead of 's are used instead of  's. Practice a few times with this technique, as this will save time on the actual exam.) 's. Practice a few times with this technique, as this will save time on the actual exam.)
|
|
|
Alternate Solutions |
99percent
2008-11-05 06:52:16 | Assuming both the hoops to be point masses concentrated at their respective center of mass, they can be considered as simple pendulums. For small oscillations, time period of a simple pendulum 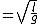 . .
Thus, the time period is proportional to the 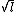 . .
Therefore, the time period of Y is 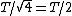
Bingo..!! |  |
|
|
Comments |
gravity
2010-11-04 23:36:45 | You can do it this way - and this is the way I did it first time around - but you might not get the same physical pendulum on the test and I'm noticing that I'm using this equation a lot of the time on practice tests, so I suggest knowing how to do it this way too:
The period for a physical pendulum is (memorize this):
T = 2 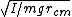
Where 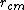 is the center of mass. is the center of mass.
The moment of Inertia is in the form of mr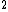 (don't care about the constant in front). The mass and one r in the moment of Inertia cancels with the denominator. So the ratio of the two pendulums is (don't care about the constant in front). The mass and one r in the moment of Inertia cancels with the denominator. So the ratio of the two pendulums is 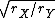 = = 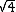 = 2 = 2
The answer is B.
A little bit extra work, but since these are practice tests, it's good to know several ways to solve these problems so that you can solve them more generally.
gravity
2010-11-04 23:42:02 |
Also note that the moment of inertia in that equation is measured from the support.
The ratio is still the same factor.
http://hyperphysics.phy-astr.gsu.edu/hbase/pendp.html
|
|  | apr2010
2010-04-08 08:23:48 | One could also use:
1) Know that 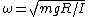 with m mass, g gravitational constant, R radius and I moment of inertia from a few problems before with the two pendulums. with m mass, g gravitational constant, R radius and I moment of inertia from a few problems before with the two pendulums.
2) Get Moment of Inertia 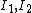 with with 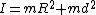
3) Get ratio 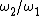 . .
|  | venus19000
2009-10-30 10:55:25 | I don't know if this is a correct approach, but I used 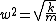 . .
This gave me 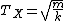
and 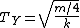 . .
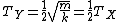
Therefore the period of Y was 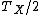 . .
flyboy621
2010-10-22 16:27:04 |
This is not correct. You got lucky.
The period depends on the size, but not the mass.
|
flyboy621
2010-10-22 16:48:52 |
At least, that is what Yosun was saying. I think Marten down below has it right.
From wikipedia, the angular frequency of small-angle oscillations for a physical pendulum is
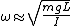
where L is the distance from the suspension point to the CM, in this case the radius for each hoop. So the period DOES depend on the mass no matter how you do it. Again, Marten got it right.
|
|  | 99percent
2008-11-05 06:52:16 | Assuming both the hoops to be point masses concentrated at their respective center of mass, they can be considered as simple pendulums. For small oscillations, time period of a simple pendulum 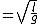 . .
Thus, the time period is proportional to the 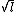 . .
Therefore, the time period of Y is 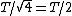
Bingo..!!
apr2010
2010-04-08 08:24:35 |
Awesome
|
ali8
2011-07-12 13:28:32 |
That's how I get at this problem.
|
|  | 99percent
2008-11-05 06:50:43 | Assuming both the hoops to be point masses concentrated at their respective center of mass, they can be considered as simple pendulums. For small oscillations, time period of a simple pendulum 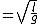 . .
Thus, the time period is proportional to the 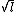 . .
Therefore, the time period of Y is 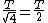
Bingo! |  | Tommy Koulax
2007-10-26 19:41:22 | I ment T/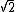 not not 
Tommy Koulax
2007-10-28 11:53:43 |
Wow, I just had a brain fart there. The factor is 4, not 2 like I was saying in my stuper.
|
|  | Tommy Koulax
2007-10-26 19:40:02 | Rx=2Ry not 4Ry. Solving the problem as done above leads to T/ . Something is not right. . Something is not right. |  | marten
2007-10-24 13:32:54 | If we have  = = 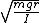
And I figure the mass moment of inertia for a hoop rotating about a point on the rim to be:
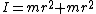 by the parallel axis theorem, I don't see how the angular frequency is the same as a pendulum. by the parallel axis theorem, I don't see how the angular frequency is the same as a pendulum.
ewhite2
2007-10-27 13:19:12 |
marten, I think you are right. However, since it is just the ratio of periods we are interested in, this extra factor of 1/2 inside the radical will cancel giving the same solution.
|
kyros
2007-10-31 16:30:33 |
Feelfree to work it out using your formula - I just did, and it comesout to T/2.
|
marten
2007-11-13 09:29:30 |
Thanks for the comments. I see what you're saying about the factors canceling out. I'll have to work it out to see for myself, but since the Nov 3rd test is finally done, and I've been studying since June, I'm not very inclined to more problems just quite yet!
|
|  | Andresito
2006-03-29 10:33:23 | There is a MimeTeX failure after the ratio of periods. The ratio is quite confusing written in that way. Thanks for the answers worked out Yosun. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
