|
GR9277 #67
|
|
|
|
|
Alternate Solutions |
oliTUTilo
2012-11-04 13:18:16 | I think that completely unpolarized light and circularly polarized light would behave the same on our filter system. That is, they would both transmit a constant intensity over filter angles.
Completely unpolarized light has components of polarization in all directions.
Circularly polarized light has two components perpendicular to each other and a quarter out of phase, creating a net rotating (or circular) polarization. But at low speeds of rotations circularly polarized light transmits polarizations of all orientations with respect to the filter.
Since there is a term of intensity that is proportional to }^2) (namely (namely )) ), and one term that is a constant (A-B), we must have one plane-polarized component and one that is either unpolarized or circularly polarized, given that we can only choose up to two types of components. It turns out that all light that is not completely plane-polarized can be described as a sum of partly plane-polarized and partly unpolarized light. Since we can't tell from the intensity formula if the constant intensity component comes from circularly polarized light or unpolarized light, we can at least conclude that the light is partly plane-polarized and partly unpolarized, as in choice (C). ), and one term that is a constant (A-B), we must have one plane-polarized component and one that is either unpolarized or circularly polarized, given that we can only choose up to two types of components. It turns out that all light that is not completely plane-polarized can be described as a sum of partly plane-polarized and partly unpolarized light. Since we can't tell from the intensity formula if the constant intensity component comes from circularly polarized light or unpolarized light, we can at least conclude that the light is partly plane-polarized and partly unpolarized, as in choice (C). |  |
|
|
Comments |
oliTUTilo
2012-11-04 13:18:16 | I think that completely unpolarized light and circularly polarized light would behave the same on our filter system. That is, they would both transmit a constant intensity over filter angles.
Completely unpolarized light has components of polarization in all directions.
Circularly polarized light has two components perpendicular to each other and a quarter out of phase, creating a net rotating (or circular) polarization. But at low speeds of rotations circularly polarized light transmits polarizations of all orientations with respect to the filter.
Since there is a term of intensity that is proportional to }^2) (namely (namely )) ), and one term that is a constant (A-B), we must have one plane-polarized component and one that is either unpolarized or circularly polarized, given that we can only choose up to two types of components. It turns out that all light that is not completely plane-polarized can be described as a sum of partly plane-polarized and partly unpolarized light. Since we can't tell from the intensity formula if the constant intensity component comes from circularly polarized light or unpolarized light, we can at least conclude that the light is partly plane-polarized and partly unpolarized, as in choice (C). ), and one term that is a constant (A-B), we must have one plane-polarized component and one that is either unpolarized or circularly polarized, given that we can only choose up to two types of components. It turns out that all light that is not completely plane-polarized can be described as a sum of partly plane-polarized and partly unpolarized light. Since we can't tell from the intensity formula if the constant intensity component comes from circularly polarized light or unpolarized light, we can at least conclude that the light is partly plane-polarized and partly unpolarized, as in choice (C). |  | swepi0
2010-11-11 21:56:37 | Correction:
I meant the identity
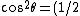(1 + \cos 2\theta))
so that we will need some unpolarized light in order that A>B, since A=B if the light is only plane polarized.
hjq1990
2012-10-02 22:55:14 |
hello guys what if A=3*B? Then A+Bcos^2\theta=3B+b(2cos^\theta+1)=2B(1+cos^2\theta)?
|
|  | narfle
2010-10-02 08:31:58 | Why couldn't it just be B - just plane polarized. As we've seen, the trig identity applied to polarization creates a "1" as a constant - and there's your A=Bcos (2theta) right there without non polarized addition
swepi0
2010-11-11 21:34:29 |
Remember that A>B whereas the trig identity
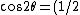(1 +\cos^2\theta))
leaves us with a constant that satisfies
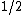 < < 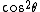 for some values of for some values of  . .
|
|  | jmason86
2009-09-07 13:00:45 | How can you have a wave that is partly polarized and partly unpolarized? That makes no sense to me when I think about wave shapes. Maybe it fits the equation, the unpolarized part will always get its intensity reduced to 1/2  and the plane polarized will be affected differently depending on and the plane polarized will be affected differently depending on  ... so the equation works. ... so the equation works.
But what the crap does this wave look like?
kroner
2009-09-28 13:42:50 |
an elliptically polarized wave.
|
kroner
2009-09-28 17:04:54 |
That is assuming the light is in a coherent plane wave. It doesn't have to be.
|
Munin
2010-04-09 19:57:04 |
Just think of it as the superposition of two waves one that is polarized and one that is partly polarized add these together (think a circle and a ellipse) and you will get the combined wave.
|
|  | neoslovakia
2007-10-22 06:45:41 | It doesnt matter for this problem, but you guys have the trig identity wrong. It should say
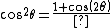}{2}) |  | Richard
2007-10-18 21:14:01 | I think there is some sentiment for more pedentry here:
According to Malus' Law, circularly polarized light has intensity ) and unpolarized light is and unpolarized light is 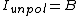 . .
Using the trig identity =1+\cos(2\theta)) , the intensity of circular polarized light is expressible as , the intensity of circular polarized light is expressible as
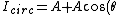)
So if we add in unpolarized light it is,
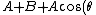=C+A\cos(\theta))
flyboy621
2010-10-22 15:39:21 |
So if A and B were equal, the incident light would be circularly polarized. Since we are given that A > B, there must be an additional unpolarized component to the incident light. Hence (C) is correct.
|
checkyoself
2011-10-04 00:00:42 |
I agree but surely in that case the answer is D? We start off with circular polarisation, identify that there's an unpolarised part due to the constant and we have answer D. I know the answer is C from ets so can someone shed light on this please.
|
|  | radicaltyro
2006-10-31 11:01:35 | What about circular polarization?
Shoshe
2006-11-03 15:18:36 |
If the incident light was completely circularly polarised, the intensity of the light passing through the rotating polaroid would be constant. The circularly polarised part of the light has transmitted intensity 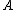 , and the plane-polarised part of the light has the oscillating intensity , and the plane-polarised part of the light has the oscillating intensity 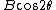 . .
|
|  | jax
2005-12-06 08:22:42 | In the exam I am looking at, it says 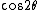 for the plane polarized part not for the plane polarized part not 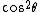 . Is that a mistake? . Is that a mistake?
yosun
2005-12-06 20:07:14 |
jax: recall the trig identity  = \cos a \cos b - \sin a \sin b) . .
|
mhas035
2007-04-05 14:41:43 |
Or 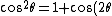)
|
|  |
|
| Post A Comment! |
You are replying to:
I think that completely unpolarized light and circularly polarized light would behave the same on our filter system. That is, they would both transmit a constant intensity over filter angles.
Completely unpolarized light has components of polarization in all directions.
Circularly polarized light has two components perpendicular to each other and a quarter out of phase, creating a net rotating (or circular) polarization. But at low speeds of rotations circularly polarized light transmits polarizations of all orientations with respect to the filter.
Since there is a term of intensity that is proportional to }^2) (namely )) ), and one term that is a constant (A-B), we must have one plane-polarized component and one that is either unpolarized or circularly polarized, given that we can only choose up to two types of components. It turns out that all light that is not completely plane-polarized can be described as a sum of partly plane-polarized and partly unpolarized light. Since we can't tell from the intensity formula if the constant intensity component comes from circularly polarized light or unpolarized light, we can at least conclude that the light is partly plane-polarized and partly unpolarized, as in choice (C). |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
