|
GR9277 #66
|
|
|
|
|
Alternate Solutions |
NoPhysicist3
2017-03-23 12:37:05 | The distance considered in 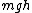 is the center of mass, therefore in this problem is the center of mass, therefore in this problem  is 5 meters. Thus, the difference in energy is is 5 meters. Thus, the difference in energy is 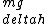  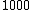  . . |  | TheXDestroyer
2007-10-02 22:36:46 | Something is not right in the official (supposed to) solution, 1st 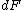 must equal must equal  gy) to get the unit of force ( to get the unit of force (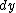 is the unit length, second thing is the the integral must be from 0 to 5 not to ten after multiplying the hole integral by 2, because you are raising only 1 half of the chain (the down half) while upper half is not touched, and multiply by 2 because every mass unit is the unit length, second thing is the the integral must be from 0 to 5 not to ten after multiplying the hole integral by 2, because you are raising only 1 half of the chain (the down half) while upper half is not touched, and multiply by 2 because every mass unit ) is being raised twice the distance from the center !!!!!!!!!!! this gives the answer 500 J !!!! this is the only correct explanation !! is being raised twice the distance from the center !!!!!!!!!!! this gives the answer 500 J !!!! this is the only correct explanation !!
I've shared the problem with physics forums you can see it on the site where you can find my solution as PDF:
http://www.physicsforums.com/showthread.php?p=1452586
|  | hamood
2007-04-04 13:01:26 | If we assume conservation of energy:
Initial PE = mgh = 20kg * g * 5m = 1000 J (average h =5m)
Final PE = mgh = 20*g*10= 2000 J
So work done = 2k - 1k =1000 J |  |
|
|
Comments |
NoPhysicist3
2017-03-23 12:37:05 | The distance considered in 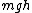 is the center of mass, therefore in this problem is the center of mass, therefore in this problem  is 5 meters. Thus, the difference in energy is is 5 meters. Thus, the difference in energy is 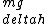  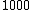 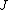 . . |  | Lamar
2016-04-10 20:09:52 | Shouldn\'t the total work be 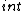  (10 - y) *g*dy, since not every piece dy is going up a distance 10 meters, but a distance (10 -y) meters?\r\n\r\nI mean you get the same value in the end, but still I want to know... (10 - y) *g*dy, since not every piece dy is going up a distance 10 meters, but a distance (10 -y) meters?\r\n\r\nI mean you get the same value in the end, but still I want to know... |  | epuma
2013-10-10 13:51:06 | If you fear integrals and forgot about center of mass:
W = mgh (use g=10m/s^2 for simplicity)
Choice (D), 2000J is the energy required to lift the entire weight of the chain 10m. We know the whole chain doesn't move that far in rolling up! We can eliminate D and E.
Choice (B), 200J, is the approximate energy required to lift just the last meter of the chain 10m. We can see the total chain-lifting energy is going to be greater than (B), if we include the energy to lift the remaining 9 meters of chain.
Thus, by process of elimination, we have choice (C).
|  | atomike238
2011-02-26 14:30:42 | Take g=10m/s^2
W = mgh
Picking up 200Kg by 10 meters take 2000J
Picking up 20Kg by 10 meters takes 200J
Rolling the chain must be in between.
The only choice is 1000J
epuma
2013-10-10 13:43:10 |
Sorry, dude! Your math is wrong.
W= mgh
Picking up 20kg by 10m takes 20*10*10 = 2000J.
|
|  | mdornfe1
2008-11-06 17:51:19 | Think about pulling the chain up all at once. The work required to do this is W=mgL, where m is the mass of the chain and L is the length. So W=2*10*10*10=2000J. Here we approximated g as 10. This is an over estimate. So we choose the next lowest answer C.
carle257
2010-04-10 01:01:32 |
This is wrong because you only move the bottom of the chain 10m. The halfway point only moves 5m and so on. You must integrate or look at the energy of the center of mass to get the correct answer.
|
|  | tensordyne
2008-11-04 19:46:20 | In order to put this problem to bed please consider the following solution. The ammount of force the chain exerts on the axel is gh, where h is the length of chain at some point in time that is hanging and g is gravity ~ 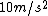 . .
The work done can be evaluated using an integral of the distance the work is done and the force exerted.
If x is the length of chain wound around the axel then  = 10 - x) . The work is then . The work is then
 dx = 1000 J) . .
insertphyspun
2011-02-06 14:01:15 |
This does not make dimensional sense. Your "force" gh has units of 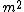 / /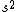 and your answer has units of and your answer has units of 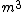 / /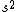 . That's like . That's like 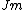 / /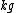 . Just saying. . Just saying.
|
|  | balla
2008-07-14 16:04:01 | Similar to previous explanations, I concentrated on the center of mass. It is a uniform chain, so the COM is initially 1/2 way along the chain (5m from pivot). When rolled up, the COM is the pivot; the change in position is 5m, the total mass is 2kg --> increase in energy = 2kg*10m/s^2 *5m = 1000J
balla
2008-07-14 16:04:50 |
Correction...2kg/m, so total of 20kg.
|
flyboy621
2010-10-22 13:51:22 |
This is absolutely the way to solve this problem. The center of mass ends up 5m higher than it was at the beginning, so the work done is just the weight of the chain times 5m.
(10m)(10m/s^2)(5m)=1000 J)
|
|  | grae313
2007-10-14 15:06:48 | The method I used is essentially equivalent to Yosun's, but I approached it a bit differently. To approximate the work, I imagined the hanging chain as being composed of 10 links, each a meter long with a mass of 2 kg. Then the total work done is comparable to the work needed to lift the bottom link up 10 meters, plus the work needed to lift the second to last link up 9 meters, plus the work needed to lift the third to last link up 8 meters plus..... until you finally lift the first link up 1 meter.
It works out to W = F*d = m*g*(10+9+8+7+...) where m is the mass of each link, or 2 kg, and g is approximately 10, so
W = 2*10*(10+9+8+7+6+5+4+3+2+1) = 20*(55) = 1100, so choice (c) is it.
I like hamood's solution better! :)
|  | TheXDestroyer
2007-10-02 22:36:46 | Something is not right in the official (supposed to) solution, 1st 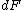 must equal must equal  gy) to get the unit of force ( to get the unit of force (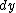 is the unit length, second thing is the the integral must be from 0 to 5 not to ten after multiplying the hole integral by 2, because you are raising only 1 half of the chain (the down half) while upper half is not touched, and multiply by 2 because every mass unit is the unit length, second thing is the the integral must be from 0 to 5 not to ten after multiplying the hole integral by 2, because you are raising only 1 half of the chain (the down half) while upper half is not touched, and multiply by 2 because every mass unit ) is being raised twice the distance from the center !!!!!!!!!!! this gives the answer 500 J !!!! this is the only correct explanation !! is being raised twice the distance from the center !!!!!!!!!!! this gives the answer 500 J !!!! this is the only correct explanation !!
I've shared the problem with physics forums you can see it on the site where you can find my solution as PDF:
http://www.physicsforums.com/showthread.php?p=1452586
marten
2007-10-24 12:14:51 |
I'm not sure what you mean by the down half. I think that you're confused about how the problem is setup. Both halves are "touched". It might to clarify that while the chain winds around the axle, the entire chain is lifted.
Describing physical setups in words can be confusing, perhaps a diagram would have been more helpful here.
Marten
|
Albert
2009-10-21 07:49:53 |
I saw your solution, and its really strange. The problem is very straight forward, you may not be reading this site anymore, I am writing for everyone.
The center of mass lies at the center of the chain, which is at 5 meters from either side, right? So we are talking about taking that part up on height. And the total mass is 20Kg.
deltaPE = work done.
W= m*g*h
W= 20*9.8*5 = 1000J (approximately)
And there is no need for calculus.
There you go big guy!
|
insertphyspun
2011-02-06 14:07:57 |
Keep track of your dimensions. g) , what you have has units of energy. The mass unit is , what you have has units of energy. The mass unit is ) . .
|
|  | hamood
2007-04-04 13:01:26 | If we assume conservation of energy:
Initial PE = mgh = 20kg * g * 5m = 1000 J (average h =5m)
Final PE = mgh = 20*g*10= 2000 J
So work done = 2k - 1k =1000 J
kroner
2009-10-06 22:02:05 |
or even quicker, by setting h=0 to be at the top:
Initial PE = mgh = 20kg * g * (-5m) = -1000 J
Final PE = 0
|
QuantumCat
2014-09-25 09:21:42 |
You don't have to assume an average height of 5 meters. Rather look at it from the center of mass point of view, since the mass density is uniform. You raise the center of mass 5 meters, so 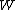 = = 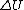 = = 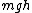 = =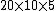 and viola. and viola.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
