|
GR9277 #61
|
|
|
Problem
|
|
\prob{61}
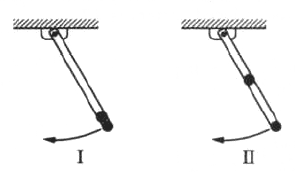
A long, straight, and massless rod pivots about one end in a vertical plane. In configuration I, shown above, two small identical masses are attached to the free end; in configuration II, one mass is moved to the center of the rod. What is the ratio of the frequency of small oscillations of configuration II to that of comfiguration I?
-
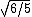
-
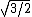
- 6/5
- 3/2
- 5/3
|
Mechanics }Small Oscillations }Small Oscillations
One can derive the frequency of small oscillation for a rigid body in general by using the torque form of Newton's Laws: 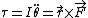 . (I is moment of inertia, r is moment arm) . (I is moment of inertia, r is moment arm)
In this case, one has a constant downwards force 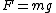 , which acts at a moment arm angle , which acts at a moment arm angle 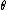 . Thus, . Thus, 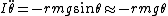 , where the approximation works if , where the approximation works if 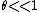 . .
The equation of motion for small angles is thus \theta) . This is similar in form to that of a simple harmonic oscillator with the angular frequency being . This is similar in form to that of a simple harmonic oscillator with the angular frequency being 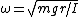 . .
Now, the problem is to find the angular frequency for each system.
One needs not worry about the rod, since it is massless and has no moment of inertia.
The moment of inertia of system I is just 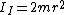 . The radius of gyration r is just . The radius of gyration r is just 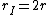 (an r for each mass). (an r for each mass).
The moment of inertia of system II is ^2 = \frac{5}{4}mr^2) . The radius of gyration r is just . The radius of gyration r is just 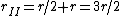 . .
Thus /(r_{I}I_{II})}=\sqrt{2\times 3 r/2/(2(5/4)\times r)}=\sqrt{6/5}) , as in choice (A). , as in choice (A).
|
|
|
Alternate Solutions |
oliTUTilo
2012-11-04 12:17:14 | I suggest using the Lagrangian formalism with the angle theta as your coordinate and the small angle approximation at hand (you just need  \approx \theta) for small for small 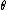 ). If you're comfortable with it, you can pretty quickly find the frequency of oscillation for the generalized pendulum of system II with pretty much no extraneous memorization. If you can't remember that the simple pendulum's frequency is ). If you're comfortable with it, you can pretty quickly find the frequency of oscillation for the generalized pendulum of system II with pretty much no extraneous memorization. If you can't remember that the simple pendulum's frequency is 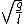 , you can generalize the distance of the intermediate mass to quickly find the frequencies for both systems. , you can generalize the distance of the intermediate mass to quickly find the frequencies for both systems.
Let  be the distance of the intermediate mass from the pivot. be the distance of the intermediate mass from the pivot.
(Lagrangian) 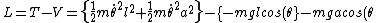\} = \frac{1}{2}m\dot{\theta}^2(l^2+a^2) + mg(l+a)cos(\theta))
(Euler Lagrange Eq) 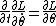
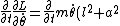 = m\ddot{\theta}(l^2+a^2))
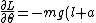sin(\theta))
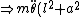=-mg(l+a)sin(\theta) \Rightarrow \ddot{\theta} = -g\frac{l+a}{l^2+a^2}sin(\theta) \approx -g\frac{l+a}{l^2+a^2}\theta \Rightarrow \omega \approx \sqrt{g\frac{l+a}{l^2+a^2}})
For system I, 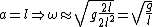 , the simple pendulum. , the simple pendulum.
For system II, 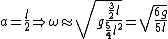
So the ratio of frequencies of System II and I is 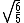
This may have looked long, but in practice you'd hopefully be better experienced with Langrangians and be able to cut corners (like knowing that out of L, only T is going to have 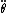 in it and only V is going to have in it and only V is going to have 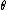 in it). Depends on how used to them you are, but you at least don't need to memorize anything you shouldn't have memorized anyways (crucial for me). in it). Depends on how used to them you are, but you at least don't need to memorize anything you shouldn't have memorized anyways (crucial for me).
BrandeisUDR
2016-02-28 00:55:55 |
The discrepancy in your negative sign before square rooting comes from the fact that the potentials should be positive in the initial Lagrangian, not negative. Otherwise, great alternate solution.
|
|  |
|
|
Comments |
deniskrasnov
2013-02-16 14:13:39 | I believe, as always with GRE, there's a way to get to the right answer by a process of elimination knowing only the basic of the formulae.
Simple pendulum:
 = = 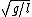
Step 1: The answer 's gotta have a square root in it, so eliminate C,D,E
Step 2: Substitute with a simpler problem: both masses at their combined center of mass ( that is instead of one mass being at half length and the second at full length we contemplate a pendulum with both masses at 3/4 length) . This gives us 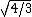
the final answer has to be less than the latter (because we have to move weights apart , thus adding an additional moment of inertia that slows down the oscillation. Eliminate B.
A. is your only remaining choice. |  | oliTUTilo
2012-11-04 12:17:14 | I suggest using the Lagrangian formalism with the angle theta as your coordinate and the small angle approximation at hand (you just need  \approx \theta) for small for small 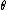 ). If you're comfortable with it, you can pretty quickly find the frequency of oscillation for the generalized pendulum of system II with pretty much no extraneous memorization. If you can't remember that the simple pendulum's frequency is ). If you're comfortable with it, you can pretty quickly find the frequency of oscillation for the generalized pendulum of system II with pretty much no extraneous memorization. If you can't remember that the simple pendulum's frequency is 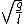 , you can generalize the distance of the intermediate mass to quickly find the frequencies for both systems. , you can generalize the distance of the intermediate mass to quickly find the frequencies for both systems.
Let  be the distance of the intermediate mass from the pivot. be the distance of the intermediate mass from the pivot.
(Lagrangian) 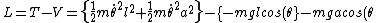\} = \frac{1}{2}m\dot{\theta}^2(l^2+a^2) + mg(l+a)cos(\theta))
(Euler Lagrange Eq) 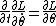
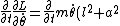 = m\ddot{\theta}(l^2+a^2))
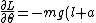sin(\theta))
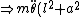=-mg(l+a)sin(\theta) \Rightarrow \ddot{\theta} = -g\frac{l+a}{l^2+a^2}sin(\theta) \approx -g\frac{l+a}{l^2+a^2}\theta \Rightarrow \omega \approx \sqrt{g\frac{l+a}{l^2+a^2}})
For system I, 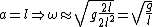 , the simple pendulum. , the simple pendulum.
For system II, 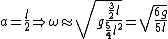
So the ratio of frequencies of System II and I is 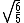
This may have looked long, but in practice you'd hopefully be better experienced with Langrangians and be able to cut corners (like knowing that out of L, only T is going to have 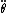 in it and only V is going to have in it and only V is going to have 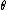 in it). Depends on how used to them you are, but you at least don't need to memorize anything you shouldn't have memorized anyways (crucial for me). in it). Depends on how used to them you are, but you at least don't need to memorize anything you shouldn't have memorized anyways (crucial for me).
BrandeisUDR
2016-02-28 00:55:55 |
The discrepancy in your negative sign before square rooting comes from the fact that the potentials should be positive in the initial Lagrangian, not negative. Otherwise, great alternate solution.
|
NoPhysicist3
2017-03-23 12:23:03 |
This is very good, however this is not what ETS wants.
|
|  | walczyk
2012-10-11 00:01:45 | I looked at this for awhile, and I know now that saying "radius of gyration" is incorrect, it should be distance from the center of mass. Radius of gyration 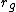 is defined as is defined as 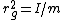 . This will get you a value of . This will get you a value of 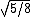 instead of instead of 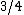 and and 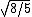 instead of instead of 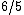 . Interestingly both are fairly accurate, that is because . Interestingly both are fairly accurate, that is because 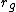 is the root mean square value of the distance from the center of mass. If the masses were not equal then your answer would actually turn out to be incorrect. I hope this clarifies thisngs for everyone else. Also I just received a new practice exam of 100 questions a few days ago. is the root mean square value of the distance from the center of mass. If the masses were not equal then your answer would actually turn out to be incorrect. I hope this clarifies thisngs for everyone else. Also I just received a new practice exam of 100 questions a few days ago. |  | Setareh
2011-11-06 13:21:43 | Could anyone tell me why I will be wrong if I go this way: There is no net torque, so L should be conserved. L(f)=L(i) ---> I(f)w(f)=I(i)w(i) ; I(i)=2ml^2 ; I(f)=ml^2+m(l/2)^2, so we will have: w(f)/w(i)=8/5 which is in the choices!!
Setareh
2011-11-06 13:30:39 |
I got my answer, I had a problem in the concept of NET torque.. I thought since the torque is not change in both states so there is no net torque, now I see I was wrong..
|
|  | Da Broglie
2011-04-07 16:54:09 | This is actually nice n simple no small angle approximations or torque equations needed.
recall the period for physical pendulums:
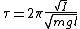 I is inertial and l is distance to center of mass I is inertial and l is distance to center of mass
invert and times by 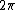 for angular frequency. for angular frequency.
for I 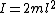 and and 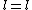
for II ^2) and and 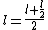
plug in and divide to get 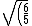})
62a
2016-10-02 23:57:45 |
Best answer. That\'s one simple and general equation that has certainly been neglected in my education. Small-angle approximations are very useful but should not be emphasized at the expense of exact formulas that are only slightly more complicated!
|
|  | Muphrid
2009-11-06 22:09:26 | Once again, Taylor expansion can come to the rescue here. If you know nothing about radii of gyration, you need only remember that any potential well can be approximated by a simple harmonic potential. In this case
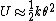
We know the potential energy exactly. For situation I, it's 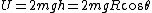 . We need only approximate this to second order. Remember . We need only approximate this to second order. Remember 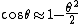 . Drop the constant order part to get . Drop the constant order part to get
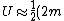 g R \theta^2)
Identify 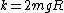 . Now we have the familiar formula for a linear oscillator of . Now we have the familiar formula for a linear oscillator of 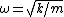 , but that doesn't apply in an angular oscillator. The mass isn't right. The angular analogue of mass is rotational inertia, , but that doesn't apply in an angular oscillator. The mass isn't right. The angular analogue of mass is rotational inertia, 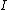 . For the first case, . For the first case, 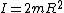 , and you get , and you get  . .
Carry this out for case II now.  . . 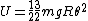 . Thus, . Thus, 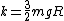 , and , and 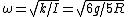 . This gets you the ratio 6/5. . This gets you the ratio 6/5. |  | ramparts
2009-08-15 19:41:19 | Alright, so the original answer has the radii of gyration off by a common factor, so the ratio stays the same. Are we really going to split hairs over this in 1.8 minutes? |  | hoyas08
2008-06-18 17:02:09 | I think georgi has it right in a previous post.
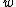 = =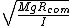 for a pendulum in general, where for a pendulum in general, where 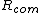 is the distance from the pivot to the center of mass along the pendulum and is the distance from the pivot to the center of mass along the pendulum and 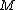 is the total mass. Then, for config. I, is the total mass. Then, for config. I, 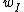 = =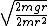 . For config. II, . For config. II, 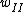 = =}{m(\frac{1}{2}r)^2+mr^2}}) . .
After the algebra, you arrive at answer (A).
gliese876d
2008-10-08 12:04:22 |
Thank you for this clarification! I knew for config 1, it should end up being the same as a simple pendulum: 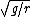 but then I was getting confused on the physical pendulum formula and mistakenly using r rather than but then I was getting confused on the physical pendulum formula and mistakenly using r rather than 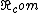
|
gliese876d
2008-10-08 12:29:22 |
Thank you for this clarification! I knew for config 1, it should end up being the same as a simple pendulum: 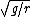 but then I was getting confused on the physical pendulum formula and mistakenly using r rather than but then I was getting confused on the physical pendulum formula and mistakenly using r rather than 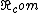
|
|  | Jeremy
2007-11-01 13:46:23 | It took me a long time, but I finally figured out what the solution is really saying.
First off, 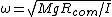 is the general equation. I explicitly show that the length is a moment arm to the center of mass. Next, I point out that "radius of gyration" ( is the general equation. I explicitly show that the length is a moment arm to the center of mass. Next, I point out that "radius of gyration" (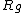 ) is not what the author really means; this is seen in how they calculate it and use it. The radius of gyration is given by ) is not what the author really means; this is seen in how they calculate it and use it. The radius of gyration is given by 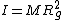 , , 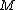 being the total mass. Thus it does not follow superposition as implicitly suggested by the solution, and, in terms of it, the frequency would still depend on being the total mass. Thus it does not follow superposition as implicitly suggested by the solution, and, in terms of it, the frequency would still depend on 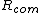 : : 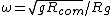 . (Clearly, the radius of gyration is not a useful quantity in this calculation - why add another length? Just use . (Clearly, the radius of gyration is not a useful quantity in this calculation - why add another length? Just use 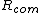 expressed as a fraction of the length of the rod). expressed as a fraction of the length of the rod).
So what's really going on? Well, look at their 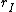 and and 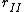 . Notice that . Notice that 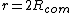 in both cases. Essentially, what they have is in both cases. Essentially, what they have is 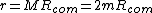 , but with the , but with the 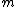 omitted. Their expression for the frequency is omitted. Their expression for the frequency is 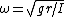 . Which, you can see, will lead to a correct answer. . Which, you can see, will lead to a correct answer.
I think a more logical solution would have 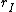 and and 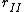 represent moment arms to the respective centers of mass, which would have the effect of halving their current values (found by represent moment arms to the respective centers of mass, which would have the effect of halving their current values (found by 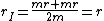 and and 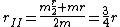 ). The moments of inertia are correct, so just use the appropriate values for ). The moments of inertia are correct, so just use the appropriate values for 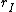 and and 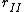 in the final equation to arrive at the solution. in the final equation to arrive at the solution. |  | theodiggers
2007-10-07 16:13:12 | What is this radius of gyration? Wikipedia doesn't give you much, why can't this be worked with CM? Georgi, its really seeming like your method fails, and its what I tried initially too. Get a CM of 3/4R, get your moment of inertia to be (9/8)MR^2, but then you get 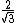 , which is fail. , which is fail.
theodiggers
2007-10-07 16:17:50 |
Sorry, I'm an idiot. Can't calculate moments of inertia with CM...
|
theodiggers
2007-10-07 16:27:47 |
...Freedman and Young gives no reason why this fails in general, only an example of its failure. Why does this fail in general?
|
|  | georgi
2007-08-26 20:52:13 | you don't have to go through the derivation and i highly doubt ets wants you to go through it in 1.7 minutes.
recall the formula for a physical pendulum st w = 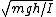 where h is the distance from the pivot to the center of mass and everything follows trivially from there. where h is the distance from the pivot to the center of mass and everything follows trivially from there. |  | sharpstones
2007-03-26 18:27:07 | If you never heard of radius gyration in mechanics (like I did learning from Taylor) then listen up! Start with:
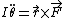
For case I the right side of the equation will be: ) since the masses are located at distance r from the hinge and the mass is since the masses are located at distance r from the hinge and the mass is 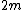
For case II the right side is:  -mgr\sin(\theta)) since you have to add the torque due to gravity acting upon each mass. since you have to add the torque due to gravity acting upon each mass.
Use small angle approximation to get an equation for the frequency with moment of inertia being 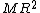 for I and for I and ^2 ) for II take the ratio and bam! for II take the ratio and bam!
chemicalsoul
2009-11-04 20:03:47 |
This is a nice alternate solution. Someone should write it out nicely and post it as alternate solution. I am challenged by how to type out the eqns otherwise i would have done it.
|
liliapunto
2013-07-14 22:34:48 |
perfect.
|
|  | am_indian
2006-11-30 09:36:20 | Wouldn\'t F=2mg?
I also get 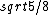
Which is not a choice. Help.
flyboy621
2010-10-22 13:32:24 |
The force of gravity acts on the center of mass of each pendulum (not on the end of the rod). System 1 has CM at the end of course:rnrn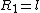 rnrnif rnrnif 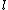 is the length of the rod. System 2 has the CM atrnrn is the length of the rod. System 2 has the CM atrnrn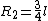 by inspection, or if you like,rnrn by inspection, or if you like,rnrn + ml) = \frac{3}{4}l) rnrnThe rnrnThe  used in the official solution should be the moment arm of the center of mass, and is NOT the same for both pendulums.rnrnThe ratio of frequencies is thenrnrn used in the official solution should be the moment arm of the center of mass, and is NOT the same for both pendulums.rnrnThe ratio of frequencies is thenrnrn}{\frac{5}{4}}} = \sqrt{\frac{6}{5}}) rn rn
|
flyboy621
2010-10-22 13:35:23 |
Not sure why my formatting didn't look the same as in the preview. Everywhere you see "rnrn" read as a double carriage return. My point is the "r" used in the official solution is not the same for both pendulums, as it is at the center of mass of each.
|
|  | am_indian
2006-11-30 09:36:09 | Wouldn't F=2mg?
I also get 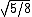
Which is not a choice. Help. |  | herrphysik
2006-08-29 21:48:05 | I believe that there is a problem with the radii of gyration you have specified. If all the mass were relocated to the radius of gyration (ROG), the moment of inertia would be the same as in the original setup. It doesn't make sense that your ROGs are larger than r, and for configuration I) all the mass already is located at one point and so the ROG should just be r. The corrections I think that need to be made are:
1) In the angular frequency equation, m=2m
2) The ROG in config. I) is just r
3) The ROG in config. II) is 3r/4
This will of course give the same answer.
dirichlet
2006-11-27 12:00:48 |
I think that is not the r of gyration for con 2 either . That would be {sqrt(5/8)}r
|
|  |
|
| Post A Comment! |
You are replying to:
I suggest using the Lagrangian formalism with the angle theta as your coordinate and the small angle approximation at hand (you just need  \approx \theta) for small 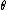 ). If you're comfortable with it, you can pretty quickly find the frequency of oscillation for the generalized pendulum of system II with pretty much no extraneous memorization. If you can't remember that the simple pendulum's frequency is 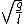 , you can generalize the distance of the intermediate mass to quickly find the frequencies for both systems.
Let  be the distance of the intermediate mass from the pivot.
(Lagrangian) 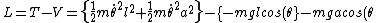\} = \frac{1}{2}m\dot{\theta}^2(l^2+a^2) + mg(l+a)cos(\theta))
(Euler Lagrange Eq) 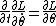
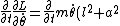 = m\ddot{\theta}(l^2+a^2))
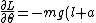sin(\theta))
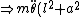=-mg(l+a)sin(\theta) \Rightarrow \ddot{\theta} = -g\frac{l+a}{l^2+a^2}sin(\theta) \approx -g\frac{l+a}{l^2+a^2}\theta \Rightarrow \omega \approx \sqrt{g\frac{l+a}{l^2+a^2}})
For system I, 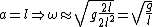 , the simple pendulum.
For system II, 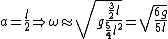
So the ratio of frequencies of System II and I is 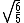
This may have looked long, but in practice you'd hopefully be better experienced with Langrangians and be able to cut corners (like knowing that out of L, only T is going to have 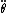 in it and only V is going to have 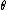 in it). Depends on how used to them you are, but you at least don't need to memorize anything you shouldn't have memorized anyways (crucial for me). |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
