|
GR9277 #53
|
|
|
Problem
|
|
\prob{53}
A particle of mass m is confined to an infinitely deep square-well potential:
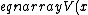&=&\infty,\;\;x\leq0,x\geq a \\ V(x)&=&0,\;\;0\lt x \lt a\end{eqnarray})
The normalized eigenfunctions, labeled by the quantum number n, are 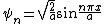
A measurement of energy E will always satisfy which of the following relationships?
-
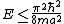
-
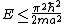
-
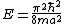
-
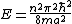
-
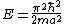
|
Quantum Mechanics }Energy }Energy
If one forgets the energy of an infinite well, one can quickly derive it from the time-independent Schrodinger's Equation  . However, since . However, since 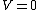 inside, one has inside, one has 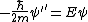 . .
Plug in the ground-state wave function ) , where , where 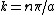 . Chunk out the second derivative to get . Chunk out the second derivative to get 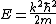 . Plug in k to get . Plug in k to get  . .
Note that 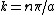 can be deduced from boundary conditions, i.e., the wave function vanishes at both ends ( can be deduced from boundary conditions, i.e., the wave function vanishes at both ends (=0) and and =0) ). The second boundary condition forces the n's to be integers. Since one can't have a trivial wave function, ). The second boundary condition forces the n's to be integers. Since one can't have a trivial wave function, 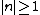 , and thus , and thus 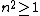 . One finds that . One finds that 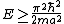 , since , since 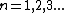 , as in choice (E). , as in choice (E).
|
|
|
Alternate Solutions |
panos85
2007-10-30 11:31:21 | The energy depends on n so it cannot be a constant. This eliminates C, D, E. Furthermore it cannot be bounded from above as it increases with n. (You can easily remember that.) So A is out. Choice B remains. |  |
|
|
Comments |
francesco
2017-09-14 20:26:58 | if you look at the eigenfunctions (in particular, at the argument of the sine) you can deduce that 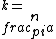 , plug it in , plug it in 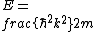 and find choice B and find choice B |  | syreen
2013-09-18 13:47:54 | The Schrodinger EQ should have hbar^2, not just hbar.
Also, as others have noted, the typed question has a typo. B. should have E>=, NOT E<= |  | Kabuto Yakushi
2010-09-04 08:58:08 | As long as you remember (which it is probably a good idea to memorize for this test) the energy in a potential well to be
E = 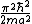
with a note that using 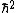 results in a two not an eight on the bottom, choice (B) is obvious. (C),(D), and (E) are to precise to satisfy the "always" criteria. results in a two not an eight on the bottom, choice (B) is obvious. (C),(D), and (E) are to precise to satisfy the "always" criteria. |  | Fizzics
2009-10-30 11:44:19 | Well I tried to post that last thing as a typo. |  | Fizzics
2009-10-30 11:43:33 | The Answer should be "B" not "E". And the answer shown in the problem as "B" is wrong. Should be E is GREATER THAN or EQUAL TO.
Typos. |  | jw111
2008-11-04 11:45:30 | Since 
and 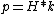 where H = h bar where H = h bar
so 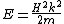
with the solution given by question,
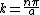
thus
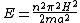 |  | Monk
2008-10-13 21:46:07 | (hbar)^2 is missing in the original presentation of the TISE, it just shows (hbar)...though most of you should know that anyhow :P |  | adenos
2007-11-02 12:49:53 | B should read E >= ....
evanb
2008-06-23 19:07:46 |
yes.
|
evanb
2008-06-23 19:11:02 |
Dammit, the preview de-TYPO-ified my entry.
Yes, (B) should be >= and not <=
and it should be the answer, not (E)
|
|  | panos85
2007-10-30 11:31:21 | The energy depends on n so it cannot be a constant. This eliminates C, D, E. Furthermore it cannot be bounded from above as it increases with n. (You can easily remember that.) So A is out. Choice B remains.
hoyas08
2008-06-16 19:52:47 |
Unfortunately, choice D has an 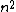 term in it, so you can't eliminate it by reasoning that the energy must depend on n. However, if you can remember that the energy of a particle in free space (V=0) is E= term in it, so you can't eliminate it by reasoning that the energy must depend on n. However, if you can remember that the energy of a particle in free space (V=0) is E= , then the 8 in the denominator of D does not make sense. , then the 8 in the denominator of D does not make sense.
|
hoyas08
2008-06-16 19:55:05 |
Unfortunately, choice D has an 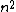 term in it, so you can't eliminate it by reasoning that the energy must depend on term in it, so you can't eliminate it by reasoning that the energy must depend on  . However, if you can remember that the energy of a particle in free space (V=0) is E= . However, if you can remember that the energy of a particle in free space (V=0) is E= , then the 8 in the denominator of D doesn't make sense, eliminating that answer. , then the 8 in the denominator of D doesn't make sense, eliminating that answer.
|
Imperate
2008-10-16 10:18:38 |
This is not true for D, D has E=n^2... which is the correct form.rnrnOne can throw away A becayse there is no upper bound to energy.rnOne can throw away C and E because they [b] are [/b] constants, which is unacceptable for the energy.rnrnThis leaves B and D, and D can only be eliminated by working out the correct coeff, as others have posted.rnrnI think this question is a bit harsh though because from elementary QM infinite square wells always have n^2 dependence so you see D whilst doing a high speed test like the GRE then you are going to pick D, well I did anyway....rnrnI
|
ramparts
2009-08-06 19:24:55 |
How does that eliminate D? D is dependent on n.
|
ramparts
2009-08-06 19:24:55 |
How does that eliminate D? D is dependent on n.
|
|  | antithesis
2007-10-05 18:17:17 | Aside from typos mentioned, the question itself has a typo, B should have equal or greater than |  | Mexicana
2007-10-04 17:46:32 | It is much easier to derive this by getting the zero point energy via Heisenberg Uncertainty Principle 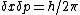 and then square this expression. Now just substitute for and then square this expression. Now just substitute for 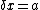 where where  is the width of the square well and then the usual expression for momentum is the width of the square well and then the usual expression for momentum ^2 = 2m E ) . .
Tommy Koulax
2007-10-29 09:53:59 |
doesn't that lead to E=^2}{2*m*a^2}) which is not an option provided? which is not an option provided?
|
|  | georgi
2007-08-26 20:20:13 | as everyone is posting the answer should be choice b, not e as written |  | welshmj
2007-07-12 15:51:47 | Choice B is the correct answer not E, but choice B on this page has a typo. It should be greater than or equal to, not less than or equal to. |  | JB
2005-12-07 02:32:15 | Isn't your answer choice (B)
jcain6
2005-12-08 19:20:24 |
It should be choice (B) because the question requires E to ALWAYS satisfy the relationship. Choice (E) only works when the potential is 0 between o and a.
|
Andresito
2006-03-27 15:43:35 |
I also think it is (B).
|
sirius
2008-06-25 13:05:18 |
the potential is 0 from 0 to a. it says so in the problem. this is a particle in an infinite square well, and answer (E) is the only answer that makes sense.
|
sirius
2008-06-25 13:09:59 |
nevermind, i misread which had the >=, i agree it is (B)
|
|  | jcain6
2005-11-22 19:06:10 | Your missing a (hbar)^2 in your numerator.
yosun
2005-11-23 02:00:51 |
jcain6: thanks for the typo-alert; it's been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
