|
GR9277 #30
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
bucky0
2007-10-04 17:11:46 | For positronium, I always assume that 6.8 eV is the binding energy. It's quick and right. |  | agaliarept
2006-11-25 16:00:09 | How can Z=1 when there is no Proton or Neutoron in positronium?
Jeremy
2007-10-30 18:11:20 |
In this formula, 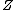 is used to represent the number of positive charges in the nucleus. In typical cases, this represents the number of protons. Here however, it is a positron that contributes the charge. is used to represent the number of positive charges in the nucleus. In typical cases, this represents the number of protons. Here however, it is a positron that contributes the charge.
|
|  | tera
2006-08-21 04:58:39 | Positron has 1/1800 the mass of hydrogen i think and i can not see the formula tha says that energey is proportional to the mass. I just can not understand the correct answer
caffeinated
2008-04-09 10:13:33 |
The Rydberg constant is E/hc =911.27E-1 angstoms. For H, divide by 1+m/M which is the reduced mass. In this case, M=m, since the nucleus is a positron, it has the same mass as the electron. Thus, the ratio of energy is 1/2.
|
dcan
2008-04-10 10:00:49 |
Oops. I left out 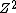 . The Rydberg constant is . The Rydberg constant is ) . I sometimes forget about Z because it's usually H with Z=1. . I sometimes forget about Z because it's usually H with Z=1.
|
Almno10
2010-11-12 14:02:03 |
The reduced mass of hydrogen atom is about me, since mu = (mp*me)/(mp + me). Do this for positronium, and see that the reduced mass is (1/2)me
|
Marian
2016-01-05 08:59:41 |
Neige Hunter: montres, nerds pourrait knock réplique Breitling Bentley Flying B plongée en apnée, il est prêt, durée du rythme cardiaque, mais tout le monde peut être dit de se concentrer sur la conception, \"et alors, regardez cette heure génial !.\"\r\n\r\nhttp://www.repliquemontresfr.eu
|
|  | astro_allison
2005-11-24 04:08:02 | are you sure z=2 here? the math doesn't work. plus it doesn't make sense that positronium, with a smaller reduced mass than helium (z=1) would have a higher z. shouldn't z=-1?
yosun
2005-11-26 01:34:59 |
astro_allison: thanks for the typo-alert; it has been corrected.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
