\prob{28}
A system is known to be in the normalized state described by the wave function
=\frac{1}{\sqrt{30}}(5Y^3_4+Y^3_6-2Y^0_6$) , ,
where the $) are the spherical harmonics. The probability of finding the system in a state with azimuthal orbital quantum number m=3 is are the spherical harmonics. The probability of finding the system in a state with azimuthal orbital quantum number m=3 is
- 0
- 1/15
- 1/6
- 1/3
- 13/15
|
Quantum Mechanics }Probability }Probability
One doesn't actually need to know much (if anything) about spherical harmonics to solve this problem. One needs only the relation \rangle|^2) . Since the problem asks for states where . Since the problem asks for states where 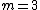 , and it gives the form of spherical harmonics employed as , and it gives the form of spherical harmonics employed as 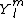 , one can eliminate the third term after the dot-product. , one can eliminate the third term after the dot-product.
So, the given wave function =\frac{1}{\sqrt{30}}\left( 5 Y^3_4 + Y^3_6 - 2Y^0_6\right)) gets dot-product'ed like gets dot-product'ed like \rangle|^2\left(\frac{1}{\sqrt{30}}\left( 5 Y^3_4 + Y^3_6\right)\right)\left(\frac{1}{\sqrt{30}}\left( 5 Y^3_4 + Y^3_6 - 2Y^0_6\right)\right)=\frac{25+1}{30}=\frac{13}{15}) , as in choice (E). , as in choice (E).
|
