|
GR9277 #27
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
94709
2007-10-16 23:57:54 | uncertainty principle.
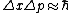
In Q.M., for any matter,
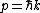
Thus, 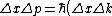=\hbar) . .
Above equations can be done in 5 seconds without writing them down.
Therefore, 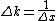 . 5 seconds in one's head. . 5 seconds in one's head.
zaijings
2009-03-13 15:21:33 |
like this solution!
|
Professor Plum
2011-07-14 14:38:57 |
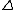 k should not depend on k should not depend on 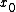 . Eliminate everything but B. . Eliminate everything but B.
|
|  | gray
2007-10-03 07:26:07 | What are Fourier variables??
underboywonder
2007-10-03 17:43:54 |
I thought about it in context of the uncertainty principle. The better the localization of the particle in space, delta x, the worse the localization in momentum space, delta k. This implies an inverse relationship, like answer B.
|
craklyn
2007-10-24 21:45:39 |
To quote my professor:
The uncertainty principle isn't anything mysterious or magical. It's simply a property of Fourier analysis!
|
Poop Loops
2008-10-25 21:07:03 |
What Yosun means by "Fourier variables" is that the Fourier transform of x-space takes you into k-space.
This is because the Fourier transform of distance-space takes you into momentum-space. And since the "k" we are referring to is from the wave equation, we can use 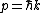 . .
If you don't know what Fourier analysis is, then you won't understand this, though, and it isn't something I can explain in a few sentences. I think my class spent a few weeks on it. Pretty important to know, though.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
