|
GR9277 #26
|
|
|
|
|
Alternate Solutions |
chrisfizzix
2008-10-06 11:48:03 | The simple jump from intuition needed to understand Yosun's solution is as follows:
Each nucleus in the sample has the same probability of decaying in the next time dt. The number of nuclei that do decay in that time is just the number of nuclei in the sample times the probability of decay in time dt. This implies that the total decay rate at any given time is proportional to the number of nuclei in the sample. So, if the count rate falls by a factor of two over a finite time interval, then we know that the population of the sample must have also decreased by a factor of two.
Thus, to solve the problem, just find the count rate at 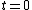 and then find the later time at which the count rate is half that of and then find the later time at which the count rate is half that of 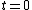 . Then the elapsed time in the half-life. . Then the elapsed time in the half-life.
Initially, the count rate is 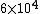 . The count rate falls to . The count rate falls to 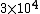 at at 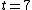 min. Thus, the half-life is 7 minutes. min. Thus, the half-life is 7 minutes. |  | troy12345
2006-11-01 13:31:36 | Though this is a more complicated way, it's the way they wanted you to do it in the problem:
The activity is given by log(dN/dt) = -L*t*log(e) + log(N0*l), where L is the inverse lifetime of the substance. So the slope of the graph is -L*log(e), which looks to be approximately -2/(40 minutes). Solving for L, we get L = -2/(40 * log(e) minutes). The halflife is given by T = ln(2)/L = log(e)*log(2)/(2/(40 * log(e) minutes)) = log(2)*20 minutes = 7 minutes. |  |
|
|
Comments |
gabep
2009-09-26 03:52:54 | This is a semi-log graph, not a log-log. ("Lab Methods}Log-Log graph") |  | jarg
2009-03-16 15:28:09 | Yosun you are one hell of a badass !
(no insult intented) |  | chrisfizzix
2008-10-06 11:48:03 | The simple jump from intuition needed to understand Yosun's solution is as follows:
Each nucleus in the sample has the same probability of decaying in the next time dt. The number of nuclei that do decay in that time is just the number of nuclei in the sample times the probability of decay in time dt. This implies that the total decay rate at any given time is proportional to the number of nuclei in the sample. So, if the count rate falls by a factor of two over a finite time interval, then we know that the population of the sample must have also decreased by a factor of two.
Thus, to solve the problem, just find the count rate at 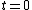 and then find the later time at which the count rate is half that of and then find the later time at which the count rate is half that of 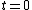 . Then the elapsed time in the half-life. . Then the elapsed time in the half-life.
Initially, the count rate is 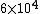 . The count rate falls to . The count rate falls to 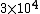 at at 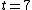 min. Thus, the half-life is 7 minutes. min. Thus, the half-life is 7 minutes. |  | ma
2007-10-13 07:11:09 | i also don't understand how you get 6000 as the inital count.
can anyone help?
Rune
2007-10-27 13:04:29 |
The way you read a log scale is for example, go where it says , that is 1x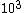 . For every horizontal line after that, the coefficient increases by 1 so it goes 1x . For every horizontal line after that, the coefficient increases by 1 so it goes 1x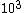 ,2x ,2x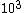 , 3x , 3x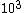 , etc etc until it gets to 10x , etc etc until it gets to 10x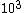 which is the same as 1x which is the same as 1x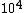 . You can see that it starts on the 6th line above , so that is 6x . You can see that it starts on the 6th line above , so that is 6x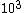
|
|  | dumbguy
2007-10-10 18:37:12 | How do we know that the initial counts is 6000? I believe my problem is in reading the log graph.
lambda
2007-10-20 16:57:08 |
dumbguy & ma: The initial count is the same as the "counts per minute" on the y-axis when time = 0. The line intersects the y-axis at "counts per minute" = 6*10^3 = 6000.
|
|  | hamood
2007-04-02 12:46:26 | The way I went about this was by choosing two points on the graph..at t=0, A=6000, and at t=20, A=800.
Then we can plug this into the formula  = = 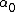 e^( e^( t) t)
 is ofcourse the decay constant, related to half-life by is ofcourse the decay constant, related to half-life by
half life = ln 2/  |  | enrico
2007-01-04 15:53:42 | The problem is modelled by
dN / dt = - k N.
And the half life is defined as 1 / k, how the hell you get this answer. The value of k is 122.5 min...
This is not physics...
andrumen1
2010-10-07 18:42:40 |
No, rememeber that 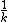 is called the characteristic time. Not the half-life, however, they are related. is called the characteristic time. Not the half-life, however, they are related.
|
|  | enrico
2007-01-04 13:29:41 | This problem is kind of weird, and I think the vertical axis should be just ln (N(t)) or the quantity of the material N(t), not the number of counts which would mean dN/dt. |  | troy12345
2006-11-01 13:31:36 | Though this is a more complicated way, it's the way they wanted you to do it in the problem:
The activity is given by log(dN/dt) = -L*t*log(e) + log(N0*l), where L is the inverse lifetime of the substance. So the slope of the graph is -L*log(e), which looks to be approximately -2/(40 minutes). Solving for L, we get L = -2/(40 * log(e) minutes). The halflife is given by T = ln(2)/L = log(e)*log(2)/(2/(40 * log(e) minutes)) = log(2)*20 minutes = 7 minutes.
Rune
2007-10-27 13:02:55 |
The way you read a log scale is for example, go where it says 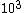 , that is 1x , that is 1x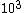 . For every horizontal line after that, the coefficient increases by 1 so it goes 1x . For every horizontal line after that, the coefficient increases by 1 so it goes 1x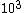 ,2x ,2x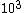 , 3x , 3x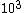 , etc etc until it gets to 10x , etc etc until it gets to 10x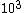 which is the same as 1x which is the same as 1x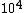 . You can see that it starts on the 6th line above . You can see that it starts on the 6th line above 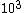 , so that is 6x , so that is 6x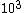
|
Rune
2007-10-27 13:04:52 |
oops, replied to the wrong person
|
apr2010
2010-04-09 02:33:31 |
There is never "the" way to do it. Somebody said, once u started calculated you lost already. Push yourself to see the obvious, it is good to know how u would do it though.
|
gravity
2010-11-07 23:51:46 |
I find often that they do intend on there being two solutions to a problem - one that takes mere seconds and another that will take much more time. It's still testing our intuition - physics isn't just about equations and proofs, we're not math majors.
Regardless, I'm realizing the last month I've spent studying physics is by far less useful than combing over these practice tests in fine detail. Good test-taking skills are a must on this test, and you have to be able to spot the "cheap" way to answer something right away.
|
|  | jax
2005-12-05 07:35:20 | Replace the E4 with E3 in the solution...
yosun
2005-12-06 20:15:42 |
jax: thanks for the typo alert; it's been corrected.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
