GREPhysics.NET: GR9277 #22

GR9277 #22

Problem

GREPhysics.NET Official Solution

\prob{22}

A simple telescope consists of two convex lenses, the objective and the eypiece, which have a common focal point P as shown in the figure above. If the focal length of the objective is 1.0 m and the angular magnification of the telescope is 10, what is the optical path length between objective and eyepieece?

0.1m
0.9m
1.0m
1.1m
10m

Optics $\Rightarrow$ }Telescope

The magnification for a telescope is related to the focal length for the eyepiece and objective by $M=f_o/f_e$ . (Note that it is the eye-piece that magnifies it. The objective merely sends an image that's within view of the eye-piece. However, magnification is inversely related to focal length.)

The problem gives angular magnification to be $M=10=f_o/f_e \Rightarrow f_e=f_o/10=.1m$ . The distance between the objective and eyepiece is the sum of the focal lengths (since the light comes from infinity). $d=f_o+f_e=1.1$ m as in choice (D).

Alternate Solutions

There are no Alternate Solutions for this problem. Be the first to post one!

Comments

kstephe6
2012-11-05 09:33:02

The faster the answer the better.

the distance is the sum of the two focal lengths, so it must be between 1 and 2 meters. Choice D. DONE

djh101
2014-08-29 16:06:32

You win.

hipparcos
2018-04-05 01:57:20

Nice one!

Reply to this comment

sky
2009-11-06 13:14:32

This can also be solved by similar triangles. Draw 2 rays passing through the common focal point of the two lenses and ending in the center of each lens. This will give two similar triangles that share equal vertical angles at the focus. the magnification factor tells us that the base of the triangle touching the objective lens should have a base length of 10 units. They give its height as the longer focal length of 1.0m. The smaller eyepiece should have a base length of 1 unit, again due to the magnification. let x be the focal length of the eyepiece. The similar triangle proportion yields,

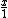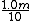
$\frac{x}{1}$ = $\frac{1.0m}{10}$

or,

x=0.1m

addition of the focal lengths gives 1.1m (D)

now that I wrote it out I think this is probably the derivation of the equation used in the solution already given. lol

Reply to this comment

emailzac
2007-11-02 18:39:17

Since the distance between the two eye pieces is the sum of the focal lengths, you know it can't be A B or C, and and the focal length of the eyepiece is usually smaller than that of the objective (at least a can't think of a case when its not) so you know the answer has to be less than 2, hence D.

Reply to this comment

Post A Comment!

Bare Basic LaTeX Rosetta Stone
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces $\alpha^2_0$ .
type this...	to get...
$\int_0^\infty$	$\int_0^\infty$
$\partial$	$\partial$
$\Rightarrow$	$\Rightarrow$
$\ddot{x},\dot{x}$	$\ddot{x},\dot{x}$
$\sqrt{z}$	$\sqrt{z}$
$\langle my \rangle$	$\langle my \rangle$
$\left( abacadabra \right)_{me}$	$\left( abacadabra \right)_{me}$
$\vec{E}$	$\vec{E}$
$\frac{a}{b}$	$\frac{a}{b}$

The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it...

All-Solutions List | Latest Comments | Unanswered Questions (Cries for Help!) |::| About

This site is not affiliated with ETS, nor is it officially endorsed (yet) by ETS. This site is the work of an individual named Yosun Chang. The solutions, sans user comments and ETS questions, are © 2005 by Yosun Chang except where noted. All rights reserved. / The comments appending particular solutions are due to the respective users. / Educational Testing Service, ETS, the ETS logo, Graduate Record Examinations, and GRE are registered trademarks of Educational Testing Service. The examination questions are © 1997 and © 2001 by ETS.

Bare Basic LaTeX Rosetta Stone