|
GR9277 #21
|
|
|
Problem
|
|
\prob{21}
A soap film with index of refraction greater than air is formed on a circular wire frame that is held in a vertical plane. The film is viewed by reflected light from a white-light source. Bands of color are observed at the lower parts of the soap film, but the area near the top appears black. A correct explanation for this phenomenon would involve which of the following?
I. The top of the soap film absorbs all of the light incident on it; none is transmitted.
II. The thickness of the top part of the soap film has become much less than a wavelength of visible light.
III. There is a phase change of 180 degrees for all wavelengths of light reflected from the front surface of the soap film.
IV. There is no phase change for any wavelength of light reflected from the back surface of the soap film.
- I only
- II and III only
- III and IV only
- I, II, and III
- II, III, and IV
|
Optics }Thin Film }Thin Film
Elimination time.
I. Can't be this, since one knows from basic thin-film theory that choice IV is right. (None of the letter choices allow for both choices I and IV.)
II. Thin film theory has 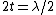 for constructive interference and for constructive interference and  for destructive interference. Thus, the thickness of the film is smaller than that of the light. (Search on the homepage of this site for more on thin film theory---it is explained in the context of other problems.) for destructive interference. Thus, the thickness of the film is smaller than that of the light. (Search on the homepage of this site for more on thin film theory---it is explained in the context of other problems.)
III. This phase change allows for the half-integer constructive interference.
IV. Phase change only occurs when light travels from a medium with lower index of refraction to a medium with higher index of refraction. Since at the back surface, the light would be going from higher to lower index of refraction, there is no phase change.
Thus, choice (E).
|
|
|
Alternate Solutions |
djh101
2014-08-29 15:59:03 | All you need to know to solve this problem is that reflection off of a surface with larger n causes a phase shift (you actually don't even need to remember whether larger or smaller n causes the phase shift, just that one of them does. From this:
A. Why would the top of the film absorb everything while the bottom doesn't?
B. If this is true, then waves reflected from the front and back would have a negligible phase shift (excluding the flip) relative to each other. When you add in the phase flip of the front reflected waves, well, you now have destructive interference.
C. Follows from B.
D. Follows from B. |  |
|
|
Comments |
Yaroslav Shustrov
2017-09-10 09:59:21 | https://physics.stackexchange.com/questions/333368/why-are-thin-soap-bubbles-colorless/333419#333419\r\n\r\nThis link is extremely useful in order to understand the question in more details. |  | socolenco_
2015-11-11 14:20:40 | For me it\'s a bit confusing the phrase in IV: \"reflected from the back surface of the soap film\". Do they mean \"refracted\"?? |  | djh101
2014-08-29 15:59:03 | All you need to know to solve this problem is that reflection off of a surface with larger n causes a phase shift (you actually don't even need to remember whether larger or smaller n causes the phase shift, just that one of them does. From this:
A. Why would the top of the film absorb everything while the bottom doesn't?
B. If this is true, then waves reflected from the front and back would have a negligible phase shift (excluding the flip) relative to each other. When you add in the phase flip of the front reflected waves, well, you now have destructive interference.
C. Follows from B.
D. Follows from B. |  | segfault
2009-09-03 12:14:04 | To clear up some confusion about II: "much less than a wavelength" does not mean it's still some half-integer multiple of  . If we have an infinitely thin film, then the *reflected* light will destructively interfere by default, because the light reflected off of the front surface of the film sees a 180 phase shift, while the light reflected off the back surface is not phase shifted; thus there is a total of a 180 phase shift--> destructive interference-->"top appears black" . If we have an infinitely thin film, then the *reflected* light will destructively interfere by default, because the light reflected off of the front surface of the film sees a 180 phase shift, while the light reflected off the back surface is not phase shifted; thus there is a total of a 180 phase shift--> destructive interference-->"top appears black" |  | Jeremy
2007-10-30 17:06:39 | When I first solved this problem, statement II bothered me because of the "much less than" phrase. The problem was, like all the other posts here, I used  (first minima) and the reasoning that goes along with it. But this leads to problems pointed out in the other posts in addition to implicitly saying (first minima) and the reasoning that goes along with it. But this leads to problems pointed out in the other posts in addition to implicitly saying 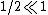 . Typically much less means at least an order of magnitude, but I knew that some thickness argument had to be used to explain the top part being black, so I went with it. . Typically much less means at least an order of magnitude, but I knew that some thickness argument had to be used to explain the top part being black, so I went with it.
The fault with the first minima approach is that it only succeeds in complete destructive interference for ONE wavelength, while the problem uses a white light source, so this cannot be the proper explanation. It turns out that "much less than" really means what it says. In fact, the film thickness is so small that the path difference for light reflecting off the back of the film is negligible, and the only thing that matters is the 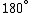 phase change for the light reflected at the front surface. Thus, regardless of the wavelength, there is always destructive interference. phase change for the light reflected at the front surface. Thus, regardless of the wavelength, there is always destructive interference.
madfish
2007-10-31 16:06:50 |
Perhaps (II) implies that there is not enough high index material to even create a thin film?
|
|  | sharpstones
2006-12-01 09:58:45 | I don't understand the explanation for II. According to your explanation the thickness will be less then the wavelength of light for both constructive and destructive interference. In fact for the constructive interference case the thickness is even smaller. So how is this an explanation for why the top is dark and the middle is bright?
Zephyr3.14
2007-04-13 20:13:07 |
I think it is because it is white light (parts of all colors of visible light) and 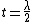 so $t << \lambda_{visible}$. This describes the thickness of the soap, which would be integral in "a correct explanation for this phenomenon." so $t << \lambda_{visible}$. This describes the thickness of the soap, which would be integral in "a correct explanation for this phenomenon."
|
Richard
2007-10-17 18:39:30 |
I think maybe Yosun meant to be more rigorous and include the general formula for constructive interference:
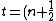\lambda)
So usually the thickness will be greater than a wavelength.
??
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
