|
GR9277 #20
|
|
|
Problem
|
|
\prob{20}
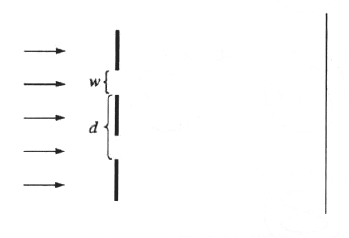
In a double-slit interference experiment, d is the distance between the centers of the slits and w is the width of the slit, as shown in the figure above. For incident plane waves, an interference maximum on a distant screen will be "missing" when
-

-

- 2d=w
- 2d=3w
- 3d=2w
|
Optics }Missing Fringes }Missing Fringes
Missing fringes in a double-slit interference experiment results when diffraction minima cancel interference maxima.
From a bit of phasor analysis, one can derive the diffraction factor  and the interference factor and the interference factor 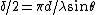 , where w is the width of the slits and d is the separation (taken from slit centers). The angles belong in the intensity equation given by , where w is the width of the slits and d is the separation (taken from slit centers). The angles belong in the intensity equation given by ^2 \cos(\delta/2)^2) . .
Thus, the condition for a double-slit diffraction minimum is given by 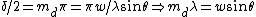 . .
Also, the condition for interference maximum is given by 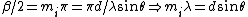 . .
Now, one needs to find the choice that allows for an integer 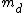 . This immediately eliminates choices (A) and (B). But, this leaves choices (C), (D), and (E). Among the remaining choices, there is only one choice that allows for slits that are smaller than the separation. This is choice (D). Take it. . This immediately eliminates choices (A) and (B). But, this leaves choices (C), (D), and (E). Among the remaining choices, there is only one choice that allows for slits that are smaller than the separation. This is choice (D). Take it.
|
|
|
Alternate Solutions |
htr
2019-09-29 15:22:47 | If this is a double slit, the distance between two slits is D=d-w. Then for interference maximum,\r\nsin(\\theta)=\\lambda*n1) . \r\n where n1 is any integer. \r\n\r\nNow actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, \r\n . \r\n where n1 is any integer. \r\n\r\nNow actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, \r\n=\\lambda*n2) .\r\n where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. \r\n\r\nThe relationship is an integer fraction and also, requires d>w.\r\n\r\nThe choice is D. .\r\n where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. \r\n\r\nThe relationship is an integer fraction and also, requires d>w.\r\n\r\nThe choice is D. |  | kstephe6
2012-11-05 07:09:44 |
Just note that d MUST be greater than w because...
d= w + (a little bit) since d is from the middle of one slit to the other. So without the "little bit extra" this two slits merge to become one.
Then note what many have shown from combining equations from the single and double slit equations...
d*(some integer) = w*(some other integer)
combine the two facts and the ONLY valid answer is D
***EXTRA INFO BELOW***
any number of integers will work here: d2=w, d3=w, d3=2w, etc... the only other restriction is that the integers must be small so as to keep in good agreement with the small angle approximation. In other words, if ETS offer d30=w12 then this would not be a valid answer. |  | Kabuto Yakushi
2010-11-12 09:36:44 | The problem says that the interference maximum is missing (in other words it is a minimum). Recalling the diffraction and interference formulas for a minimum (dark screen):
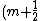\lambda=dsin(\theta)) equ. 1: interference minimum equ. 1: interference minimum
\lambda=wsin(\theta)) equ. 2: diffraction minimum equ. 2: diffraction minimum
Dividing equation 1 by equation 2 and solving one gets (D). m has to be 1, since 0 would get an undefined result. |  | nitin
2006-11-18 22:45:00 | One easy way to solve this problem is as follows.
The idea is that we need a minimum of the single-slit diffraction to coincide with a maximum of the double-slit interference pattern (which results in a "missing" interference maximum).
The angular locations of the minima of the single single-slit diffraction pattern (which modulates or envelopes the double-slit diffraction pattern) are given by:
=m_1\lambda) , where , where 
The angular locations of the maxima (bright fringes) of the double-slit interference pattern are given by:
=m_2\lambda) , where , where 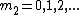
Take the ratio of the 2 equations:
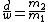 . .
Now, it is obvious that 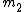 will be in general greater than will be in general greater than 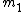 , since we have several interference maxima inside a diffraction maximum. Also, , since we have several interference maxima inside a diffraction maximum. Also, 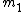 and and 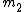 are integers. The only instance which satisfies these 2 conditions is choice (D). are integers. The only instance which satisfies these 2 conditions is choice (D).
|  |
|
|
Comments |
htr
2019-09-29 15:22:47 | If this is a double slit, the distance between two slits is D=d-w. Then for interference maximum,\r\nsin(\\theta)=\\lambda*n1) . \r\n where n1 is any integer. \r\n\r\nNow actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, \r\n . \r\n where n1 is any integer. \r\n\r\nNow actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, \r\n=\\lambda*n2) .\r\n where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. \r\n\r\nThe relationship is an integer fraction and also, requires d>w.\r\n\r\nThe choice is D. .\r\n where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. \r\n\r\nThe relationship is an integer fraction and also, requires d>w.\r\n\r\nThe choice is D. |  | htr
2019-09-29 15:18:15 | If this is a double slit, the distance between two slits is D=d-w. Then for interference maximum sin(\\theta)=\\lambda*n1) where n1 is any integer. Now actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, where n1 is any integer. Now actually there are two slits so, to have a minimum at some point, all the waves should be cancelled each other (consider derivation of single slit diffraction minimum, in this case the equivalent distance is d). So, =\\lambda*n2) . where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. Relationship is an integer fraction and also, requires d>w. The choice is D. . where n2 is an odd number. \r\n\r\nThen we have, d/(d-w) = n2/n1. Relationship is an integer fraction and also, requires d>w. The choice is D. |  | mahmoud
2017-09-25 23:41:25 | It is so simple but tricky as well . As d is from the centre to the center , and there is a separation distance between the slits, d must be longer than we w. Then the only valid answer is D |  | djh101
2014-08-29 15:40:47 | The two slits can't overlap. Such an obvious condition that just didn't occur to me... |  | Ole
2013-10-31 17:45:02 | This sinc modulated with cos
single slit w*sin(th) = m*lamb
min m = 1 ,2 3
first min at angle th1 w*sin(th1)=lamb
with in this min there are 2*L max coming from the double "slit zero width"
double "slit zero width"
d*sin(tho) = l/2*lamb
min l = 1, 3 5
max at l = 0, 2 4
With in sin(th1) there are d*sin(th1) = L/2*lamb L max one disappears L-1 at same angle w*sin(th1) = lamb
d/w =(l-1)/2 for each l=L 0, 2, 4 6 there is max
d/w=3/2 is one of them |  | Ole
2013-10-31 17:41:28 | This sinc modulated with cos
single slit w*sin(th) = m*lamb
min m = 1 ,2 3
first min at angle th1 w*sin(th1)=lamb
with in this min there are 2*k max coming from the double "slit zero width"
double "slit zero width"
d*sin(tho) = l/2*lamb
min l = 1, 3 5
max at l = 0, 2 4
With in sin(th1) there are d*sin(th1) = L/2*lamb M max one disappears K-1 at same angle w*sin(th1) = lamb
d/w =(l-1)/2 for each l=L 0, 2, 4 6 there is max
d/w=3/2 is one of them
|  | kstephe6
2012-11-05 07:09:44 |
Just note that d MUST be greater than w because...
d= w + (a little bit) since d is from the middle of one slit to the other. So without the "little bit extra" this two slits merge to become one.
Then note what many have shown from combining equations from the single and double slit equations...
d*(some integer) = w*(some other integer)
combine the two facts and the ONLY valid answer is D
***EXTRA INFO BELOW***
any number of integers will work here: d2=w, d3=w, d3=2w, etc... the only other restriction is that the integers must be small so as to keep in good agreement with the small angle approximation. In other words, if ETS offer d30=w12 then this would not be a valid answer.
kstephe6
2012-11-05 07:14:43 |
oops on the "EXTRA" info... I should have written other possible answers would be d=2w, d=3w, 2d=3w, 3d=4w... and a poor answer due to the small angle approximation would be 12d=30w... sorry
|
|  | walczyk
2012-10-15 13:24:38 | I think the problem is asking for when the interference maximum coincides with the diffraction maximum, thus making it "disappear." Solving for this condition gets you the correct answer. I found the exact answer for intensity, and the only time diffraction minima cancel out is when the slit is an integer multiple of the distance between them. See: http://web.mit.edu/8.02t/www/materials/StudyGuide/guide14.pdf |  | Kabuto Yakushi
2010-11-12 09:36:44 | The problem says that the interference maximum is missing (in other words it is a minimum). Recalling the diffraction and interference formulas for a minimum (dark screen):
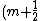\lambda=dsin(\theta)) equ. 1: interference minimum equ. 1: interference minimum
\lambda=wsin(\theta)) equ. 2: diffraction minimum equ. 2: diffraction minimum
Dividing equation 1 by equation 2 and solving one gets (D). m has to be 1, since 0 would get an undefined result.
pam d
2011-09-23 18:08:27 |
This approach is incorrect because you have not used the condition of an interference maximum combined with a diffraction minimum. You used the condition for an interference minimum. You must arrive at a "missing" interference maximum, i.e. it was supposed to be there but is not.
Also, the m's do not have to be the same here. Just look at the Fresnel interference pattern of a double slit and you'll see that many interference minima and maxima occur within the diffraction pattern.
I hope this post was clear enough.
|
Tbot
2011-10-25 05:47:09 |
The question asks "when is a maximum missing?" That must mean that the double slit maximum coincides with a single slit minimum. To solve the problem, we need to assume that the angle  corresponds to a Maximum of the double slit diffraction and Minimum of the single slit diffraction. It is incorrect to select an angle for which both are at a minimum. corresponds to a Maximum of the double slit diffraction and Minimum of the single slit diffraction. It is incorrect to select an angle for which both are at a minimum.
|
cz
2012-11-04 22:53:22 |
This argument is wrong. The interference maximum is missing means simply that it is there but cannot be seen. It cannot be seen because it has been made dark by the diffraction minimum. (The diffraction effect has masked the interference effect.)
The interference pattern always is always attenuated by the diffraction envelope.
|
kstephe6
2012-11-05 07:11:02 |
this aligns the minima... exactly the opposite of what you want to do here.
|
adhumunt
2015-10-20 21:27:24 |
This is perhaps the simplest and most intuitive method to solving this problem.
|
RusFortunat
2015-10-22 12:16:49 |
Thank you
|
|  | chemicalsoul
2009-11-04 11:44:04 | for double slit diffraction one can remember this little formula;
if d=n*w , d and w as in the question and n is the missing interference maximum form the center with the condition that d is greater than w. In this particular question for a distant screen, (D) satisfies it. |  | pavamanacs
2009-09-16 02:06:33 | how can we explain uncertainity principle using this
cz
2012-11-04 22:54:47 |
Uncertainty principle really has nothing to do with this..
|
|  | Richard
2007-10-17 18:32:26 | I think that there are two important pedagogical aspects to this problem.
First being, that it shows how the GRE problems usually require you to use your "physics brain." What I mean is, you often have to rule out a few possibilities due to a "physical" argument of some sort: A few of the choices in this problem give you slit widths that are larger than the distance between them.
Second, I think the phrase "an interference maximum...will be missing when..."
is particularly important. Note they didn't say, "Find THE distance for which an interference maximum will be missing..."
So it's not necessarily the FIRST missing interference maximum or the last (of course there is no last possible...). As with many problems there is some degree of ambiguity.
Anyway, I hope this helps someone.
|  | nitin
2006-11-18 22:45:00 | One easy way to solve this problem is as follows.
The idea is that we need a minimum of the single-slit diffraction to coincide with a maximum of the double-slit interference pattern (which results in a "missing" interference maximum).
The angular locations of the minima of the single single-slit diffraction pattern (which modulates or envelopes the double-slit diffraction pattern) are given by:
=m_1\lambda) , where , where 
The angular locations of the maxima (bright fringes) of the double-slit interference pattern are given by:
=m_2\lambda) , where , where 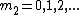
Take the ratio of the 2 equations:
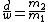 . .
Now, it is obvious that 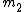 will be in general greater than will be in general greater than 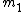 , since we have several interference maxima inside a diffraction maximum. Also, , since we have several interference maxima inside a diffraction maximum. Also, 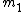 and and 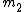 are integers. The only instance which satisfies these 2 conditions is choice (D). are integers. The only instance which satisfies these 2 conditions is choice (D).
jw111
2008-11-03 22:28:33 |
I think that m2 > m1 is from the fact that
d > w for double-slit
if d |
lin
2015-09-06 10:45:34 |
This answer is pretty clear to understand
|
|  | blackholepioneer
2006-10-29 18:19:39 | I\\\\\\\'m a little confused about your derivations, so I did the following, check and see if I messed up somewhere.
 =distance between slits =distance between slits
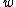 =width of a slit =width of a slit
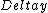 =distance on the screen =distance on the screen
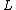 =distance between 2 screens =distance between 2 screens
 =wavelength =wavelength
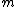 =an interger =an interger
max: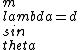
min:\\\\\\\\lambda=d\\\\\\\\sin\\\\\\\\theta)
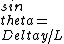

for small 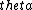 , , 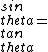 , thus , thus
\\\\\\\\lambda=d\\\\\\\\lambda/w) , the , the  s cancel, so we have s cancel, so we have
w) . .
The only 2 choices that satisfy this condition are C and D, we pick D, because 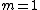 is the central maximum, so is the central maximum, so 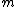 needs to be larger or equal to 2. needs to be larger or equal to 2.
|  | dgelbi
2006-10-25 00:00:54 | the conditions are mixed. The first one is related with the interference (cos is the interference term) and the second one with the difraction (sin is the diffraction term) |  | astro_allison
2005-11-20 16:33:06 | isn't there an easier way to solve this? When I took this as a practice test, I did this:
we know that (m+.5)(lambda)=dsin(theta) for it to be dark, and (change in y)=wsin(theta), where w= width of slit. for small angles, sin(theta) ~ (theta).
solving each eq for (theta) & setting them equal, we have:
[(lambda)(m+.5)/d]=[(change in y)/w]
solve for it in terms of w and d, and neglect (lambda) for now:
w=[(change in y)/(m+.5)]*d
y~m, so take it to a first order, ie m=1.
then:
w=[1/(3/2)]d or w=(2/3)d...
2d=3w.
this might be a wrong approach though...
tau1777
2008-11-03 16:46:13 |
i like this approach opposed to the other ones, to be honest there just to confusing. and this is the method i was trying to use when doing it,but i was missing the crucial fact that delta y = sin(theta)w. thanks for this post.
i also think, as a general comment, that the simple solution is always the best one, as long as it gets you the right answer. it's a timed exam and i think the ETS wants us to be able to see these easier solutions.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
