|
GR8677 #98
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
casseverhart13
2019-08-09 06:13:52 | This problem is so difficult! tree service |  | yis5125
2015-09-04 09:22:09 | I tried to solve this problem in an alternative way, which is less simple and convenient than the official solution on the site, but unfortunately failed to get the correct answer. I can\'t find my mistake and I am quite baffled. I shall deeply appreciate if someone would like to offer me help soon!\r\n\r\nMy solution is to integrate the intensity of electric field E at the point P first, and then integrate the electric potential at the same point. \r\n\r\nAssume the linear electric density 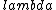 ,\r\nQ= ,\r\nQ=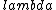 L, dQ= L, dQ=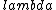 dx,\r\n\r\ndE= dx,\r\n\r\ndE=^2}) = =^2}) dx, \r\n\r\nE= dx, \r\n\r\nE=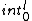 ^2}) dx,\r\n\r\nApplying the substitution method, set u=x+l, du=dx, so\r\nE=k dx,\r\n\r\nApplying the substitution method, set u=x+l, du=dx, so\r\nE=k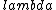 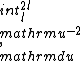 =k =k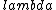 [ [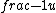 ]= ]=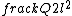 .\r\n\r\nHence, V= .\r\n\r\nHence, V= = = 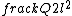 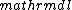 = =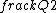 [ [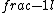 ]= ]=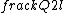 .\r\n\r\nSo my answer is the choice B. \r\n\r\nCan someone tell me where I did wrong? .\r\n\r\nSo my answer is the choice B. \r\n\r\nCan someone tell me where I did wrong? |  | yis5125
2015-09-04 08:42:18 | I tried to solve this problem in an alternative way, which is less simple and convenient than the official solution on the site, but unfortunately failed to get the correct answer. I can\'t find my mistake and I am quite baffled. I shall deeply appreciate if someone would like to offer me help soon!\r\n\r\nMy solution is to integrate the intensity of electric field E at the point P first, and then integrate the electric potential at the same point. \r\n\r\nAssume the linear electric density 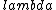 ,\r\nQ= ,\r\nQ=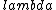 L, dQ= L, dQ=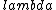 dx,\r\ndE= dx,\r\ndE=^2}) \r\n = \r\n =^2}) dx, \r\nE= dx, \r\nE=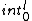 ^2}) dx,\r\nApplying the substitution method, set u=x+l, du=dx, so\r\nE=k dx,\r\nApplying the substitution method, set u=x+l, du=dx, so\r\nE=k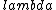 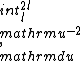 =k =k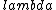 [ [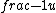 ]= ]=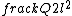 .\r\n\r\nHence V= .\r\n\r\nHence V= \r\n = \r\n = 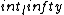  .\r\nFinally, there comes out infinity of the electric potential. \r\n\r\nCan someone tell me where I did wrong? \r\n .\r\nFinally, there comes out infinity of the electric potential. \r\n\r\nCan someone tell me where I did wrong? \r\n |  | Lawliet_Black
2013-08-24 03:44:40 | If I'm thinking of this correctly, the answer should be greater than 1/2 (it would be as if all of the charges were at 2l) and less than 1 (as if all the charges were at l), so you can eliminate all but C and D. |  | anum
2010-11-11 12:21:44 | i don't get it why not b?
anum
2010-11-11 12:23:10 |
i mean e. why involve integration.
|
flyboy621
2010-11-15 20:40:24 |
You have to integrate because each dq contributes differently to the potential according to its distance from P.
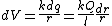
Integrating over  from from 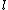 to to 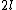 gives (D). gives (D).
|
|  | rohit
2008-11-07 07:52:44 | firstly , the limits are from 0 to l ( over the charge distribution )
second, the the integrand is dq/(x+l)
wittensdog
2009-07-28 10:51:15 |
Either method should be equivalent. In the official solution, x represents the distance from the point P to a point on the rod, since the potential goes like 1/x from a point charge. The closest point is a distance l away, and the furthest is a distance 2l away. So integrating over the rod entails integrating from l to 2l, since the integration variable is x.
Your method merely represents a substitution x -> x + l, with the limits accordingly shifted. You use x instead to represent not the distance from the point P to a point on the rod, but as a variable that ranges over the length of the rod, and thus indeed, x+l becomes the denominator in the potential, since now this is the distance to point P. Both methods yield the correct answer. Depending on the order of integration you could have a sign difference, but clearly that doesn't matter for finding the right answer in this problem.
Actually, in order to evaluate the integral you propose, you would likely make a substitution of the form u = x + l, so that you would have an integral of the form du / u, and then shift the limits of integration so that they were in terms of u. This would restore the original integral in the official solution.
|
jmracek
2009-10-16 19:17:56 |
i think rohit's approach is more intuitive
 = \int_0^l \frac{kdq}{r-r'} = k\lambda\int_0^l \frac{dx}{2l-x} = k\lambda ln(2))
|
spacemanERAU
2009-10-21 18:10:13 |
it is more intuitive but requires a little more work
|
|  | a19grey2
2008-11-04 16:41:12 | To clarify, the correct answer is D. |  | Andresito
2006-03-21 00:48:48 | V = k * integral (dq / x) , in the first expression. |  |
|
| Post A Comment! |
You are replying to:
I tried to solve this problem in an alternative way, which is less simple and convenient than the official solution on the site, but unfortunately failed to get the correct answer. I can\'t find my mistake and I am quite baffled. I shall deeply appreciate if someone would like to offer me help soon!\r\n\r\nMy solution is to integrate the intensity of electric field E at the point P first, and then integrate the electric potential at the same point. \r\n\r\nAssume the linear electric density 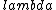 ,\r\nQ= 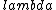 L, dQ= 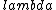 dx,\r\ndE= ^2}) \r\n = ^2}) dx, \r\nE= 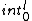 ^2}) dx,\r\nApplying the substitution method, set u=x+l, du=dx, so\r\nE=k 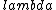 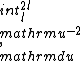 =k 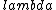 [ 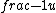 ]= 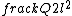 .\r\n\r\nHence V=  \r\n = 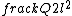 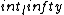  .\r\nFinally, there comes out infinity of the electric potential. \r\n\r\nCan someone tell me where I did wrong? \r\n |
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
