|
GR8677 #92
|
|
|
|
|
Comments |
casseverhart13
2019-08-19 09:43:53 | This problem helps me more. Thanks for your sharing! Tree Solutions Lake Mary |  | whereami
2018-04-09 03:39:50 | My memory goes that selection rule regards only delta l and delta ml. I didn\'t even believe selection rule works on those aspects. \r\nTurns out that delta s =0 is one of the selection rules. And there are none regarding n values. My thought against A is that n could be 0. But of course that is not forbidden by the selection rules. |  | kevintah
2015-09-09 09:05:11 | This site has more information including the full derivation and results. http://quantummechanics.ucsd.edu/ph130a/130_notes/node422.html\r\n There is no selection rule for spin as mentioned\r\n
sam16
2015-10-20 14:12:33 |
page not found!
|
NoPhysicist2
2017-03-19 11:36:32 |
http://quantummechanics.ucsd.edu/ph130a/130_notes/node422.html
|
|  | flyboy621
2010-11-15 19:54:48 | 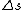 is always 0, and is always 0, and 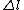 is always +/- 1. Therefore is always +/- 1. Therefore 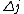 is also +/- 1. Thus (B) and (E) are compatible and (D) is not. is also +/- 1. Thus (B) and (E) are compatible and (D) is not. |  | dvarjas
2010-10-06 07:52:54 | My oppinion after much thougth about why D is incorrect and E correct: If there are two electrons on the same orbit, their spatial wave functions are symmetric, therefore they form a spin singlet with s=0. It could happen, that an unpaired electron with s=1/2 jumps to a half filled orbit with another electron with s=1/2, making a transition from s=1/2+1/2=1 to s=0, or the reverse process could also happen. But the total angular momentum j is conserved for the whole system, photon takes away j=1, so 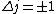 as in (E). But as in (E). But 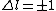 and and 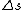 cannot be greater than 1 for a single electron process, cannot be greater than 1 for a single electron process, 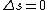 is needed for conservation of total angular momentum. So the only process allowed is that an unpaired electron jumps to an empty orbit. is needed for conservation of total angular momentum. So the only process allowed is that an unpaired electron jumps to an empty orbit.
gman
2010-11-11 23:11:59 |
How about this...
When the electron transitions, 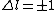 . Since it's an electron, and it doesn't change spin, . Since it's an electron, and it doesn't change spin, 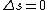 . So . So 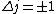 . .
Now the photon has spin 1, and has no orbital angular momentum (right? what's it.. orbiting?) So 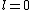 , , 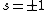 , and thus , and thus 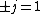 . All consistent with the above selection rules. The orbital angular momentum lost becomes spin angular momentum. Thus, . All consistent with the above selection rules. The orbital angular momentum lost becomes spin angular momentum. Thus,
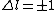
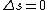
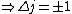
|
|  | hanmas
2008-04-11 20:48:21 | s always equals to 1/2 for electron, so there is no such thing as 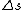 = -1. = -1.
lattes
2008-08-05 22:40:54 |
Good observation!
|
Poop Loops
2008-11-05 21:43:06 |
But can't you go +1/2 or -1/2? I thought that's what it meant. Either way, it still doesn't work so that's the answer.
|
wittensdog
2009-07-28 08:17:19 |
Indeed, s is the magnitude of spin, and m_s would be the value of it's projection along a given axis, often denoted z by convention. It's the same as how l is the magnitude of orbital angular momentum, and m_l is it's projection along an axis. Since in the answers they did make note of l vs. m_l (and not simply just m), I believe they meant to distinguish between s and m_s. While m_s can change for an electron, between -1/2 and 1/2, the MAGNITUDE of spin for any particle is fixed, so having any change in s is nonsensical. I actually didn't even notice this myself, and was originally thinking it meant m_s. Good observation!
|
|  | keflavich
2005-11-10 11:04:25 | Since 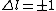 , and , and 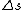 is unrestrictied (i.e. it can equal zero), E is compatible with electric dipole selection rules. This whole question is about photon emission: photons are emitted when electrons change energy levels, and it\'s the change in energy level\'s that\'s being restricted. is unrestrictied (i.e. it can equal zero), E is compatible with electric dipole selection rules. This whole question is about photon emission: photons are emitted when electrons change energy levels, and it\'s the change in energy level\'s that\'s being restricted.
yosun
2005-11-10 11:33:18 |
if 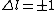 and and 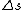 is unrestricted, then shouldn't is unrestricted, then shouldn't 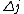 also be unrestricted? also be unrestricted?
|
keflavich
2005-11-10 12:05:46 |
Maybe my logic was wrong. In retrospect, I think any 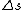 restriction should be incompatible with electric dipole emission since changes in the spin are related to hyperfine splitting. If you were to consider only electric dipole emission by excited states of atoms, I think you must assume that spin doesn't change and therefore restriction should be incompatible with electric dipole emission since changes in the spin are related to hyperfine splitting. If you were to consider only electric dipole emission by excited states of atoms, I think you must assume that spin doesn't change and therefore 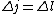 . Any . Any 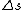 would not involve or be involved in a transition between excitation states of an atom. I think it would require two emissions - one hyperfine, one electric dipole - to change both would not involve or be involved in a transition between excitation states of an atom. I think it would require two emissions - one hyperfine, one electric dipole - to change both 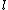 and and  . .
Anyway, 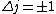 certainly wouldn't violate any selection rules, but certainly wouldn't violate any selection rules, but 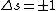 would prevent any transition that did NOT change the spin of an electron, which is not a condition of electric dipole emission. would prevent any transition that did NOT change the spin of an electron, which is not a condition of electric dipole emission.
|
keflavich
2005-11-10 17:48:31 |
Right, valid point (though maybe you're refering to C). Instead of arguing more, I decided to look it up... http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydazi.html />
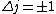 is a valid restriction for some case (though I don't really understand what a j=0 state would be since is a valid restriction for some case (though I don't really understand what a j=0 state would be since 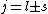 ), there is no spin restriction. As it turns out, hyperphysics claims that in photon emission the electron spin quantum number doesn't change, so perhaps the C transition (in 0177:82) is allowed because ), there is no spin restriction. As it turns out, hyperphysics claims that in photon emission the electron spin quantum number doesn't change, so perhaps the C transition (in 0177:82) is allowed because 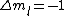 ? ?
|
keflavich
2005-11-10 17:53:07 |
Ignore my comments, just check out the website. I've contradicted myself enough on this problem that my answers are probably unreliable.
|
mhas035
2007-04-12 23:10:09 |
The electric dipole operator is not dependant on the spin of the electron so for electirc dipole transitions, transitions between different spin states will give a probability of zero
|
|  | Buli
2005-11-08 21:14:27 | If there is no selection rule for spin, then there would be no for j too. Recall that j=l+s. I was wondering this is because the photon emission obeys the conservation of spin momentum so that delta s is zero. Can anybody tell your opinion? Thanks.
mpdude8
2012-04-19 16:56:25 |
You said it yourself: j = l +s, there IS a selection rule for l (it must change by 1) but no selection rule for s, thus j must change with l. If there was a selection rule for s, you may be able to have the change in l and s cancel perfectly.
|
|  | snimi1
2005-11-05 00:54:17 | The official answer is D, which I tend to agree because there is no spin related selection rule.
yosun
2005-11-05 23:09:46 |
Thanks snimi1 for the correction!
|
athithi
2008-04-10 22:50:20 |
i am wondering about the option A ..how n can take negative values ?
|
thebigshow500
2008-10-14 10:56:46 |
Same question on choice (A)...the subject GRE test is coming soon, anyone care to explain?
|
kobayashi_maru
2008-10-15 07:31:37 |
The problem specifies emission of photons by excited states. For an electron to emit a photon, it has to drop from a higher excited state to a lower one (or ground state). Thus, 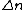 is negative. is negative.
|
thebigshow500
2008-10-15 18:45:29 |
I am an idiot. I thought 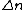 has to be a positive value. But it should be has to be a positive value. But it should be 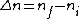 = negative value. = negative value.
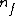 = lower state = lower state
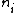 = higher state = higher state
Thanks a lot!
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
