|
GR8677 #91
|
|
|
Problem
|
|
 |
Optics }Bragg Reflection }Bragg Reflection
Bragg diffraction is basically the wavelength change of a wave impinging two adjacent layers of the crystal. More specifically, it relates the wavelength difference of the incident wave on the top layer to that of the reflected wave on the lower layer. The distance between layers (``lattice planes", in Solid-State-Speak) is 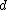 , and the angle of incidence is , and the angle of incidence is 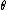 . The change in wavelength is thus a simple geometry problem, the result being the celebrated Bragg Reflection Relation, . The change in wavelength is thus a simple geometry problem, the result being the celebrated Bragg Reflection Relation,
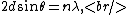
where  corresponds to the order of the reflection. corresponds to the order of the reflection.
The problem supplies the following numbers
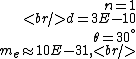
and if one recalls the de Broglie relation, 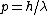 , one has, in general, , one has, in general, 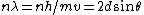 . Plugging in some numbers, one finds that . Plugging in some numbers, one finds that 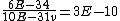 , since , since 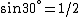 , and where the approximation scheme to battle the no-calculators-allow requirement is shown. Thus, one has , and where the approximation scheme to battle the no-calculators-allow requirement is shown. Thus, one has 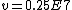 , which is very close to choice (D). , which is very close to choice (D).
The problem .
|
|
|
Alternate Solutions |
chrisfizzix
2008-10-03 14:32:17 | I feel that the posted solution lacks a bit of transparency; this is the same solution but reformatted.
Bragg Scattering gives the result
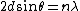
and the DeBroglie relation gives
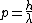 . .
First-order reflection lets us set 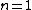 , also the relation usually fails if n > 1 anyway, so we can rearrange to write , also the relation usually fails if n > 1 anyway, so we can rearrange to write
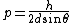
The answer in E is greater than  , so we can get rid of that. All of the other answers are non-relativistic (even for D, , so we can get rid of that. All of the other answers are non-relativistic (even for D, 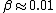 ) so we can just use ) so we can just use 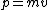 . .
Solving this, we get

Plugging in values gives a result closest to D. |  |
|
|
Comments |
casseverhart13
2019-08-16 13:14:48 | thanks for the very useful problem! Gainesville Pressure Washing University |  | anmuhich
2009-03-21 15:03:39 | I don't know hardly any optics, but one can eliminate A, B and E because they are completely unreasonable speeds for an electron. D seems the most plausible out of the two left. |  | student2008
2008-10-14 06:07:56 | Since the orders of magnitude in answers differ a lot, we can even don't get use of 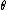 & Bragg condition. All we use is & Bragg condition. All we use is 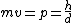 , since , since 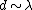 (actually, in this problem (actually, in this problem 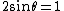 , so we even obtain the exact result). , so we even obtain the exact result).
wittensdog
2009-07-28 08:06:08 |
Just out of curiosity, I wanted to test how well this strategy would work in general. For 30 degrees the answer is indeed pretty much exactly on. To have the 2 * sin(theta) term introduce as much as a factor of ten, the incident angle would have to be as small as about 2.86 degrees, just grazing the surface. Even with a factor of ten, you should be able to discriminate between answers enough to get the right one.
Sounds like a powerful trick to me! I'll have to keep it in mind if I ever get stuck on a problem with wave phenomenon in general.
|
wittensdog
2009-07-28 08:10:07 |
Also, if you wanted to see if it could introduce a factor of ten the other way, as in to create a decrease from the correct answer, you'd end up with theta = arcsin( 5 ). So need to worry about that!
|
rahat90
2014-09-11 03:43:11 |
This is a useful trick!
|
|  | chrisfizzix
2008-10-03 14:32:17 | I feel that the posted solution lacks a bit of transparency; this is the same solution but reformatted.
Bragg Scattering gives the result
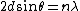
and the DeBroglie relation gives
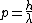 . .
First-order reflection lets us set 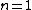 , also the relation usually fails if n > 1 anyway, so we can rearrange to write , also the relation usually fails if n > 1 anyway, so we can rearrange to write
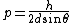
The answer in E is greater than  , so we can get rid of that. All of the other answers are non-relativistic (even for D, , so we can get rid of that. All of the other answers are non-relativistic (even for D, 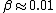 ) so we can just use ) so we can just use 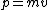 . .
Solving this, we get

Plugging in values gives a result closest to D.
luwei0917
2014-04-02 08:08:41 |
thanks.
|
|  | madfish
2007-11-02 19:04:53 | if one knows electrons travel very fast to give off x-rays, but not faster than the speed of light...one can elminate all but C & D
chrisfizzix
2008-10-03 14:13:43 |
The electron isn't radiating X-rays - the spacing between lattice planes in the crystal has been previously measured using X-rays. Thus, the threshold for X-ray emission by an electron has nothing to do with this problem.
Also, electrons need both high energy and some kind of accelerating force to emit X-rays, such as the magnetic field from a bending magnet in a synchrotron.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
