|
GR8677 #90
|
|
|
|
|
Alternate Solutions |
casseverhart13
2019-08-20 12:22:40 | Helpful problem. Lucky me I found your site by accident. towing service |  | BillNyeTheRussianSpy
2018-05-22 03:06:49 | I think, notationally, it is easier to have 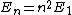 . But it still comes out the same.\r\n\r\n . But it still comes out the same.\r\n\r\n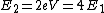 implies implies 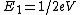 |  | BillNyeTheRussianSpy
2018-05-22 03:06:49 | I think, notationally, it is easier to have 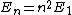 . But it still comes out the same.\r\n\r\n . But it still comes out the same.\r\n\r\n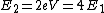 implies implies 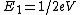 |  |
|
|
Comments |
casseverhart13
2019-08-20 12:22:40 | Helpful problem. Lucky me I found your site by accident. towing service |  | BillNyeTheRussianSpy
2018-05-22 03:06:49 | I think, notationally, it is easier to have 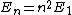 . But it still comes out the same.\r\n\r\n . But it still comes out the same.\r\n\r\n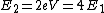 implies implies 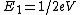 |  | BillNyeTheRussianSpy
2018-05-22 03:06:49 | I think, notationally, it is easier to have 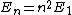 . But it still comes out the same.\r\n\r\n . But it still comes out the same.\r\n\r\n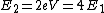 implies implies 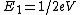 |  | Moush
2010-09-19 06:20:35 | Yosun, in the 2nd paragraph you have "load" instead of "node". Richard mentioned it but didn't classify it as a typo so you probably didn't see it.
I just noticed that the preview button resets the classification to NEC.
Thanks for this site! |  | neon37
2008-11-06 14:49:13 | I solved this slightly differently,
We know,

and De Broglie wavelength,
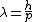
Plug this into the E and we find out,
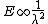
So wavelength is doubled going from this state to ground state so the Energy has to be a quarter so  . .
wittensdog
2009-07-27 13:10:26 |
That works in this case, but only because it makes sense to talk about a specific wavelength. The infinite square well is weird in the sense that because there are definite energy states in a region where there is no potential energy, you have E = p^2/2m for a set of definite energies, you end up with states that have a definite magnitude of momentum. So then these definite momentum magnitude states correspond to a precise wavelength. Normally there would be a spread in p, but the square well has this nice feature. I didn't even really think about this until a semester after taking my QM course, when I read it in the appendix of my statmech book. There was actually kind of an interesting derivation of the infinite square well properties, just making reference to the idea of de Broglie waves being fit inside the well. But if you were to try to apply the method to another potential, I imagine it would not be so successful. It makes a lot of sense thinking about the fourier transform. Inside the well you have pure sine waves, and the fourier transform of a pure sine wave with some frequency w just has two delta spikes at +/- w, each normalized with a factor of 1/2 to make the total probability equal to 1. Of course there would be mixing in from other wavelengths if you were to consider the entire range of x values, outside of -a and a, because then you have a wave pulse.
|
wittensdog
2009-07-27 13:11:30 |
But I guess my point was, I always thought that was a really interesting property of the square well.
|
|  | FortranMan
2008-10-30 07:41:56 | Try not to confuse this with the harmonic oscillator where the ground state is n=0. |  | jesford
2008-04-03 17:57:00 | Even if you can't remember the infinite-square-well energies, the problem asks for the LOWEST possible energy... so it can't be more than the 2 eV energy given for the diagram. This rules out choices D and E. Also, recall that the particle can't have zero energy, so the only options left are B and C.
jesford
2008-04-03 17:58:41 |
oops I guess 1 eV is less than 2, eh?
|
|  | Richard
2007-11-01 12:37:50 | You wrote "load," but you should have written "node."
:)
realcomfy
2008-11-01 09:50:32 |
I also believe that it should state that the particle has 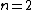 nodes thus giving us nodes thus giving us 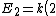^2 = 4k)
|
realcomfy
2008-11-01 09:51:31 |
Check here and correct me if I am wrong
http://en.wikipedia.org/wiki/Image:Particle_in_a_box_wavefunctions.png
|
gt2009
2009-06-25 17:17:22 |
2 antinodes, not nodes
|
wittensdog
2009-10-08 11:37:54 |
This isn't very scientific, but instead of fretting over nodes vs. anti-nodes, I always just remember that the state number is the number of "bumps."
|
IRFAN
2011-08-18 02:25:34 |
Actually you ppl confuse node i thimk it might be loops
|
|  | grae313
2007-10-07 19:01:27 | Alternately, knowing 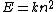 we can write we can write
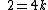
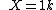
Divide the first equation by the second and solve for x. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
