|
GR8677 #59
|
|
|
|
|
Alternate Solutions |
blackwind
2011-10-16 14:47:35 | Simply use limits to evaluate 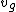 : :
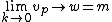

Derivative by 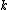 then gives you the limits then gives you the limits |  |
|
|
Comments |
ernest21
2019-08-23 02:03:34 | Easy, but even easier if you look at it this way: a is absolutely meaningless because the zero of potential is arbitrary. dere.exe
danielsw98667
2019-10-21 06:08:11 |
The group velocity of these waves approaches Zero as k → 0 and c as k → ∞. The answer is letter E. best merchant services
|
|  | varsha
2016-02-19 15:14:17 | In option A,why have they taken w.r.t w.As k tends to 0,we should see Vg right??\r\nVg should be infinity,not w.. |  | blackwind
2011-10-16 14:47:35 | Simply use limits to evaluate 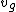 : :
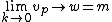

Derivative by 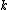 then gives you the limits then gives you the limits
danielsw98667
2019-10-21 06:23:39 |
As k → 0, vg = 0\r\nAs k → ∞, vg = c\r\nsince m ≪ → \\\\v_g=\\frac{c^2 k}{\\sqrt{c^2 k^2}}=\\frac{c^2 k}{c^2 k^2}=c\r\nCincinnati Channel Letter Signs
|
|  | anmuhich
2009-03-21 09:45:15 | I used a similar approach as chrisfizzix. I didn't even remember much at all about group velocities but I did remember it's like the velocity of a particle. I didn't know what a propogation vector was per se but I relized that it must be directly related to the group velocity just by the name of it. This idea combined with the idea that it shouldn't move faster than the speed of light led me to E. Of course it's much better to know the formula for the group velocity and solve as shown above, but if all else fails use a little common sense and you'll come out ahead of the 1/4 point off for each wrong answer. |  | chrisfizzix
2008-10-03 13:16:24 | I solved this by some quick common sense. The group velocity is just the velocity of the particle associated with the wave motion. For any physical system, the group velocity can never be larger than c. Thus, any answer that has 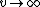 is out - goodbye A, B, D. The propagation vector k is absolutely related to group velocity, and if is out - goodbye A, B, D. The propagation vector k is absolutely related to group velocity, and if 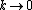 then the wave better not be going anywhere. Thus, C is out, leaving E. then the wave better not be going anywhere. Thus, C is out, leaving E.
neon37
2008-11-05 00:07:59 |
Hi I read this article in wiki http://en.wikipedia.org/wiki/Group_velocity that seems to suggest group velocity can be greater than speed of light. It says quote:
Since the 1980s, various experiments have verified that it is possible for the group velocity of laser light pulses sent through specially prepared materials to significantly exceed the speed of light in vacuum. However, superluminal communication is not possible in this case, since the signal velocity remains less than the speed of light.
well i can sorta visualize it but if someone is expert in this subject could you please explain it so that I can confirm.
Thanks
|
neo55378008
2012-09-06 10:43:35 |
neon37, if you read the next line in the Wiki entry, it says that while the group velocity is greater than c, communication is still less than c. I don't claim to be an expert on this, but from my understanding the vocabulary we use is changing. Physicists have stopped using the term matter/energy when talking about relativity, and lately have been saying information. Information cannot travel faster than the speed of light. It seems like a subtle difference, but I believe this saves relativity and causality.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
