|
GR8677 #54
|
|
|
Problem
|
|
 |
Electromagnetism }Dielectric }Dielectric
Recall the following equations,
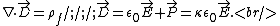
Also, recall the relation between bound charge and polarization,
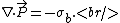
Use the divergence theorem on the above equations to apply the elementary Gauss' Law to the region,


But, since 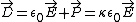 , one has , one has 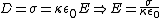 . Plug that into the other relation for D (and use the result for P from above) to get, . Plug that into the other relation for D (and use the result for P from above) to get, 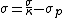 . Thus, . Thus, 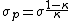 , as in choice (E). , as in choice (E).
|
|
|
Alternate Solutions |
hooverbm
2012-10-01 09:32:47 | Super fast way to do this.
This is exactly what a capacitor is (one side of it), with a dielectric wedged inbetween the plates.
Compare capacitor in vacuum with one with dielectric. More field lines pass through the capacitor in vacuum. However, with the dielectric, some field lines are "intercepted" by *negative* charges that are induced.
The induced charge that accumulates is never going to exceed the surface charge density of the conductor. For most dielectric materials, the induced charge density must be lower.
Therefore, we know that the solution must be negative and the induced charge density be smaller than the surface charge density of the conductor.
Pick a number for K, find the one that gives a fraction of the amount *and* is negative.
Thus E. |  | flyboy621
2010-11-14 21:27:59 | As K approaches 1, the dielectric does not conduct at all, and the charge approaches 0.
As K gets very large, the dielectric acts like a good conductor, and the charge approaches minus sigma.
The only solution that matches both criteria is (E). |  | Herminso
2009-09-21 19:02:57 | The charge induced on the dielectric must be negative since  >0 on the conductor (remember images method), in addition that induced charge must be less than >0 on the conductor (remember images method), in addition that induced charge must be less than  for a dielectric which have $k>1$, thus the only answer choice is (E). for a dielectric which have $k>1$, thus the only answer choice is (E). |  | sevensixtwo
2006-07-31 22:25:33 | Whoa, dude! This is actually nice and simple. No divergence theorem needed.
use gauss law for dielectrics with cylindrical surface. because E=0 in the conductor there is only flux through one end of the cylinder go gauss law becomes:
D A = sigma A, so D = sigma
then, D = k e0 E (Griff. eq 4.31)
so E = sigma / (k e0)
plug those values into:
e0 E + P = D (Griff. eq. 4.21)
simplify to get P = [sigma (k-1)/k] (z-hat)
then dot by n-hat = z-hat to get the bound surface charge in the conductor. then the bound charge in the dielectric just has the opposite charge so its choice E.
also, if you're not sure that we were solving for the bound charge in the conductor remember that the field in the dielectric has the same sign as the free charge. since we said the field was positive, the bound charge in the dielectric has to be opposite to the positive sign of the bound charge in the conductor. |  | StudyTime
2005-11-09 21:06:49 | Alternatively, you can check the limits. SigmaBound->0 for k->1, SigmaBound->SigmaSurface for k->infinity. Only choice (E) survives. |  |
|
|
Comments |
fredluis
2019-09-17 02:05:02 | The solution given above is wrong. Purely qualitatively, by Ampere\'s Law, B field will be in the +/- Z direction at point P. The energy flux vector S points outward (obviously). Thus E is in the XY plane (Orthogonal Triad). tree removal |  | ernest21
2019-08-23 02:03:04 | The one thing I\'m seeing over and over again is that every physics GRE problem has a quick and simple way to do it. Sometimes it\'s a calculation trick, sometimes it\'s just knowing something by heart. infinitode |  | hooverbm
2012-10-01 09:32:47 | Super fast way to do this.
This is exactly what a capacitor is (one side of it), with a dielectric wedged inbetween the plates.
Compare capacitor in vacuum with one with dielectric. More field lines pass through the capacitor in vacuum. However, with the dielectric, some field lines are "intercepted" by *negative* charges that are induced.
The induced charge that accumulates is never going to exceed the surface charge density of the conductor. For most dielectric materials, the induced charge density must be lower.
Therefore, we know that the solution must be negative and the induced charge density be smaller than the surface charge density of the conductor.
Pick a number for K, find the one that gives a fraction of the amount *and* is negative.
Thus E. |  | trippy_hippie
2011-05-20 10:44:43 | Alternatively, on can solve this using two simple premises. 1) The dielectric constant is always greater than or equal to unity. 2) The induced charge density should be of opposite sign and lesser in magnitude than the bound charge density. POE can then be used against the choices.
A) This is the opposite sign, but the induced charge density will be greater in magnitude than the bound charge density.
B) Although it will be lesser in magnitude, this induced charge will not be opposite in sign.
C) This will be greater in magnitude and have the same sign. (Double Wrong!)
D) This will be greater in magnitude and have the same sign. (Double Wrong...again!)
E) This will have a sign opposite the induced charge and will be lesser in magnitude. (Also, it's our last choice and final hope!) |  | Fily
2011-04-07 06:10:59 | simply put k=1 than sigma should be zero. |  | flyboy621
2010-11-14 21:27:59 | As K approaches 1, the dielectric does not conduct at all, and the charge approaches 0.
As K gets very large, the dielectric acts like a good conductor, and the charge approaches minus sigma.
The only solution that matches both criteria is (E).
Manuel Abad
2012-04-05 12:22:41 |
You're wrong. K>1 says the dielectric is less and less similar to a conductor, so there's more and more BOUNDED charge (sigma is just the free charge). As K tends to 1, the dielectric resembles more and more to a conductor, so bounded charge must go to zero. Your limits are right, but your physics is wrong.
|
|  | xrpx
2010-10-06 14:52:55 | If K=1 then polarisation charge is not, thus (E)
ypeels
2015-08-11 07:22:50 |
You win
|
|  | Prologue
2009-11-06 18:57:04 | If you like you can break this problem up into parts. First look at what the E field would be without the dielectric, namely
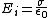
Then with the dielectric in place
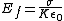
Now the difference in the two must be due to an electric field generated by the bound charges. Keep in mind that the only effect the dielectric has is to generate these bound charges nothing else, so the E field generated by the bound changes is not subject to the dielectric constant. The bound E field is given by
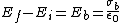
By doing this you get
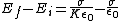
So
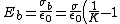 = \frac{\sigma}{\epsilon_{0}} \left (\frac{1-K}{K} \right))
This means the bound surface charge is given by
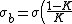)
ihatejackson
2011-09-26 19:22:39 |
nice
|
|  | abacus
2009-10-06 23:29:13 | Here's another soln:
The bound charges in a dielectric plate redistribute so that  (This is why capacitance is proportional to K) (This is why capacitance is proportional to K)
Inside the dielectric, it looks like there's a surface with charge density is 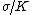
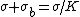
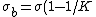) |  | Herminso
2009-09-21 19:02:57 | The charge induced on the dielectric must be negative since  >0 on the conductor (remember images method), in addition that induced charge must be less than >0 on the conductor (remember images method), in addition that induced charge must be less than  for a dielectric which have $k>1$, thus the only answer choice is (E). for a dielectric which have $k>1$, thus the only answer choice is (E).
alemsalem
2010-09-21 06:00:49 |
also the bound charge must be zero when k is equal to 1
which is to say no charge would be induced when it's vacuum!
|
|  | nitin
2006-11-16 08:34:36 | Let 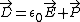 . .
Take the divergence of this expression:
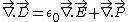 . .
Let the permittivity of the dielectric be 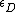 . Then, . Then, 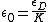 . .
Now,
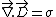 , ,
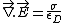 , and , and
 . .
Substitute these in the divergence equation, to get:
}{K}) , which is choice (E). , which is choice (E).
|  | bterranova
2006-10-19 14:08:52 | The divergence of the polarization is related to the total charge density, not the surface charge density.
CMSmonkey
2009-11-06 13:09:27 |
I agree!
|
|  | sevensixtwo
2006-07-31 22:25:33 | Whoa, dude! This is actually nice and simple. No divergence theorem needed.
use gauss law for dielectrics with cylindrical surface. because E=0 in the conductor there is only flux through one end of the cylinder go gauss law becomes:
D A = sigma A, so D = sigma
then, D = k e0 E (Griff. eq 4.31)
so E = sigma / (k e0)
plug those values into:
e0 E + P = D (Griff. eq. 4.21)
simplify to get P = [sigma (k-1)/k] (z-hat)
then dot by n-hat = z-hat to get the bound surface charge in the conductor. then the bound charge in the dielectric just has the opposite charge so its choice E.
also, if you're not sure that we were solving for the bound charge in the conductor remember that the field in the dielectric has the same sign as the free charge. since we said the field was positive, the bound charge in the dielectric has to be opposite to the positive sign of the bound charge in the conductor.
flutefreek
2007-10-02 02:46:27 |

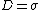
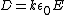 (Griff. eq 4.31) (Griff. eq 4.31)
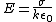
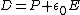 (Griff. eq 4.21) (Griff. eq 4.21)
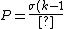}{k} \hat{z})
|
Jeremy
2007-10-24 11:25:22 |
Minor correction: 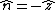 , since this is the "outward" direction for the dielectric. Therefore, you don't have to hand wave the sign! , since this is the "outward" direction for the dielectric. Therefore, you don't have to hand wave the sign!
|
walczyk
2012-11-08 15:55:52 |
The rationale for why we have a term DA, instead of perhaps D2A, is subtle for me. For a gaussian surface the integral is over the area of the surface, which in this case is a cylinder. This is assuming flux is across the entire surface, however because the field inside a conductor is always zero then the flux is zero, so the side of the gaussian cylinder inside the conductor does not contribute to the integral. We further simplify things by allowing the length of the cylinder to approach zero, so the sides also do not contribute to the integral. so we have D*pi*r^2 = Q_f=\sigma*pi*r^2. Then proceed as the OP describes. If you take the integral over both ends of the cylinder then your answer will be off by a factor of 1/2.
|
|  | StudyTime
2005-11-09 21:06:49 | Alternatively, you can check the limits. SigmaBound->0 for k->1, SigmaBound->SigmaSurface for k->infinity. Only choice (E) survives.
thebigshow500
2008-10-14 01:35:04 |
I will try your method if I were you.
However, by fitting k ->  to (E), we get -Sigma. Is this making any sense? to (E), we get -Sigma. Is this making any sense?
|
gotfork
2008-10-16 15:01:48 |
I think this makes sense, -Sigma effectively cancels the surface charge since we don't expect to see any total surface charge since both materials are conductors.
|
a19grey2
2008-11-03 22:22:55 |
We expect to see -(Sigma) because the opposite charge will go to towards the charge on the conductor (like charges are repelled).
Also, both materials are not conductors. When k-> THEN the dielectric acts as a conductor. When k->1 is when the slab labeled "dielectric" is acting like vacuum would.... and since there can be no bound charges in vacuum, the bound charge THEN the dielectric acts as a conductor. When k->1 is when the slab labeled "dielectric" is acting like vacuum would.... and since there can be no bound charges in vacuum, the bound charge 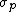 ->0. ->0.
|
archard
2010-09-04 09:39:34 |
I think this is the best approach. It's important to remember that the lower limit on K is 1, because K is defined as (1+chi), where chi is the electric susceptibility. So, when K is 1, there is essentially no dielectric there at all, and the bound surface charge should go to 0. E is the only choice that does this.
|
|  | StudyTime
2005-11-09 21:02:38 |
varsha
2016-02-19 09:57:20 |
enu
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
