fredluis
2019-09-17 02:01:31 | Opposite sides of the cube have the same potential, so as we go across the cube we start with the potential at V and end with the potential at V. Since there are no charges inside, there is nothing to change the potential so it must be constant all the way across. tree removal |  |
ernest21
2019-08-23 02:02:58 | At first I thought you may be wrong, but here is a simple thought experiment that shows you must be correct: space marshals 2 |  |
santo35
2014-07-31 03:59:21 | Isnt the electric field varying at all points "P" ? (since it is an oscillation ?
And if so are we considering the maximum value of variation here ? |  |
santo35
2014-07-31 03:58:36 | Isnt the electric field varying at all points "P" ? (since it is an oscillation ?
And if so are we considering the maximum value of variation here ? |  |
santo35
2014-07-31 03:56:44 | isnt that field varying at all points P ? rnrnOr is it that we are considering only the maximum value of the variation at all points P and comparing them ? |  |
849444209
2013-10-16 07:48:56 | |  |
natec
2013-08-18 17:46:35 | Say point P were in the XZ plane and  was the angle BELOW the x-axis. Would the electric field now be in the XZ plane with maximum magnitude at was the angle BELOW the x-axis. Would the electric field now be in the XZ plane with maximum magnitude at 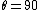 ? I can't see why not because of the symmetry of the arrangement. ? I can't see why not because of the symmetry of the arrangement. |  |
SillyMan
2013-06-19 20:17:23 | The solution given above is wrong. Purely qualitatively, by Ampere's Law, B field will be in the +/- Z direction at point P. The energy flux vector S points outward (obviously). Thus E is in the XY plane (Orthogonal Triad). At 90 degrees, one "sees" the highest acceleration, which means that the power flowing past P is the highest at theta = 90 degrees. The answer was implied by Maxwell's equations and the Larmor result. |  |
flyboy621
2010-11-14 21:12:43 | I don't know if this will help anybody, but...
You can imagine standing at the origin, holding one end of a rope, the other end of which is at point P. Then you start waving the end of the rope back and forth along the x-axis. The waves in the rope will be oriented in the xy-plane and be maximum when P is on the y-axis, i.e. theta is 90 degrees.
The analogy works because EM waves are transverse, just like waves in a string.
deafmutemouse
2011-09-20 14:10:54 |
This analogy is awesome! Thanks!
|
OptimusPrime
2017-04-08 04:47:54 |
This is really helpful! The point of fastest velocity of the rope shaking happens when crossing the y-axis, which is maximum E amplitude in this case.
|
|  |
faith
2010-11-11 23:14:24 | here's another way to look at it.
cross product! v=ExB since particle is moving along the x direction, E field max should only be along y.
faith
2010-11-11 23:18:35 |
yikes.. sorry, this solution is wrong. i had it by luck.
|
|  |
wittensdog
2009-09-28 21:43:42 | The one thing I'm seeing over and over again is that every physics GRE problem has a quick and simple way to do it. Sometimes it's a calculation trick, sometimes it's just knowing something by heart.
In this case, I strongly recommend remembering two basic facts which have a good chance of coming up on any test:
1.) an oscillating charge never radiates in the direction of its oscillation axis
2.) the polarization of an oscillation charge is parallel to the oscillation axis
Don't bother wondering why (at least not for the sake of the GRE), just memorize that. If you use those two pieces of information, you immediately see that the E-field should be in the xy plane from the restriction on the polarization, and also that the maximum field strength should be at 90 degrees, since along the x axis it has no magnitude, and increases as you move away from the x axis.
So far, in all of my studying, I've never come along a GRE problem that required a formula with more than 3 or 4 terms in it. Maybe that's a slight exaggeration, but you get the point.
apr2010
2010-04-09 09:22:19 |
Does not the dipol radiate also in the z-direction? This looks like a trap again, as the Point P lies only in the x-y-plane, meaning A and B are not even available.
|
|  |
Herminso
2009-09-22 13:56:33 | For a electric dipole =qd\cos {(\omega t)}\hat{x}) we have: we have:
![\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\theta}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}](/cgi-bin/mimetex.cgi?\vec{E}=-\frac{\mu_0qd\omega^2}{4\pi}(\frac{\sin {\theta}}{r})\cos {[\omega(t-r/c)]}\hat{\theta}) and and ![\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\theta}}{r})\cos {[\omega(t-r/c)]}\hat{\phi}](/cgi-bin/mimetex.cgi?\vec{B}=-\frac{\mu_0qd\omega^2}{4\pi c}(\frac{\sin {\theta}}{r})\cos {[\omega(t-r/c)]}\hat{\phi})
Thus the oscilation of the electric field is in the xy-plane and the maximum is at 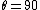 , just the y-axes. , just the y-axes.
Herminso
2009-09-22 14:22:02 |
Where  is measured from the positive x-axes on the xy-plane. is measured from the positive x-axes on the xy-plane.
|
|  |
a19grey2
2008-11-03 22:14:06 | I recommend just learning what the picture of an oscillating dipole looks like. rnhttp://en.wikipedia.org/wiki/DipolernrnIt'll help you later in your physics life anyway...
physicsisgod
2008-11-05 20:32:44 |
Here's a cool video of it:
http://www.vis.uni-stuttgart.de/ufac/dipole/
|
|  |
jw111
2008-09-14 11:09:42 | You see the maximum OSCILATION of charge when you stand on y axis, and minimum oscilation when you stand on x axis.
=> max field take place on y axis
the ocilation is on x-y plane, the field line wave mainly on x-y plane.
=>oscilating field on x-y plane |  |
ee7klt
2005-11-11 04:54:58 | hi,
since oscillations happen only in the x-y plane, the E-field vector thus cannot have components in the z-direction. This eliminates (A) and (B).
The minimum occurs when you're looking directly down the x-axis i.e. 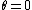 (all you see is the infinitesimal tip of the field vector which doesn't look like it'll generate any waves coming towards you) - this eliminates (D). From here, I guess you'll need to remember that the field goes as (all you see is the infinitesimal tip of the field vector which doesn't look like it'll generate any waves coming towards you) - this eliminates (D). From here, I guess you'll need to remember that the field goes as 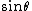 to narrow it further down to (C). to narrow it further down to (C).
Simplicio
2009-03-31 17:13:47 |
It's oscillating along the x-axis so you can't just say "it is in the x-y plane". It might as well been the x-z plane ...
|
|  |
physicsDen
2005-11-09 22:04:58 | is it me, or is this a poor attempt at a solution?
alpha
2005-11-09 22:15:19 |
it's a quick and dirty way to arrive at the right answer.
|
mpdude8
2012-04-19 14:19:49 |
Definitely a poor attempt at a solution, but a great solution for the sake of the GRE.
You do not have the time to use any formulas on a problem like this. It really has to be 100% intuition in order for you to finish. You don't have 3-4 minutes to think of a relevant formula, you just have to see the problem and know what to look for instinctively.
Thus, many of the solutions to these problems on this site are not rigorous whatsoever, but the GRE couldn't care less about rigor.
|
|  |
