|
GR8677 #48
|
|
|
Problem
|
|
 |
Atomic }Transition }Transition
Transitions go from state one to another state that's completely unique relative to the first state. If both initial and final states have spherically symmetrical wave functions, then they have the same angular momentum. This is forbidden.
|
|
|
Alternate Solutions |
casseverhart13
2019-09-05 06:23:55 | Many thanks conducive towards the great problem. click here\r\n |  | jgramm
2014-09-23 21:58:30 | If they're both spherical, they're both in the s shell (think back to those silly pictures of orbitals in high school chem).
If 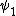 transitioned to transitioned to 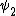 , both electrons (fermions) would occupy the same state, which is not allowed by the Pauli exclusion principle. , both electrons (fermions) would occupy the same state, which is not allowed by the Pauli exclusion principle.
Thus, D is the obviously the answer without having to worry about any of that selection rule nonsense that nobody ever remembers (or maybe it's just me). |  |
|
|
Comments |
casseverhart13
2019-09-05 06:23:55 | Many thanks conducive towards the great problem. click here\r\n
danielsw98667
2019-10-21 06:53:45 |
D is the most obvious answer. altera
|
|  | ernest21
2019-08-23 02:02:11 | The information you share is very useful. It is closely related to my work and has helped me grow. Thank you! tapiriik |  | joshuaprice153
2019-08-09 06:32:28 | Thanks a lot for sharing us about this update. Hope you will not get tired on making posts as informative as this. computer repair Ocala |  | idoubt
2015-10-19 06:55:38 | I think the answer has to do with the fact that photons are a spin 1 particle and it cannot have the m = 0 state. So to emit a photon the two wave functions must have an angular momentum difference  . This is not possible if both are S shell. . This is not possible if both are S shell. |  | jgramm
2014-09-23 21:58:30 | If they're both spherical, they're both in the s shell (think back to those silly pictures of orbitals in high school chem).
If 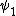 transitioned to transitioned to 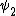 , both electrons (fermions) would occupy the same state, which is not allowed by the Pauli exclusion principle. , both electrons (fermions) would occupy the same state, which is not allowed by the Pauli exclusion principle.
Thus, D is the obviously the answer without having to worry about any of that selection rule nonsense that nobody ever remembers (or maybe it's just me).
Baharmajorana
2014-10-15 06:04:04 |
I agree with u, I can't remember too
|
James6M
2014-10-15 20:36:49 |
Um, what?
There is only one electron in a hydrogen atom, so I don't know why you are talking about "both." And just because both wavefunctions are s-shells, that doesn't mean they are the same wavefunction. They can have different n.
So, no, the Pauli exclusion principle has nothing to do with this question.
|
|  | a_coiled_atom
2011-07-16 12:35:34 | I thought of it in terms of the selection rules , . If the initial state has , which corresponds to spherical symmetry in the wavefunction, then according to these the final state must have , which is not spherically symmetric. |  | a_coiled_atom
2011-07-16 12:34:28 | I thought of it in terms of the selection rules 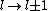 , , 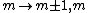 . If the initial state has . If the initial state has 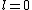 , which corresponds to spherical symmetry in the wavefunction, then according to these the final state must have , which corresponds to spherical symmetry in the wavefunction, then according to these the final state must have  , which is not spherically symmetric. , which is not spherically symmetric.
pam d
2011-09-24 11:31:55 |
This is how it's done.
|
|  | thebigshow500
2008-10-13 22:12:48 | Can anyone explain if other choices are something to do with wave function? (e.g. parity, orthogonality, etc.) Or are these choices just simply nonsense? :(
kroner
2009-10-16 12:06:41 |
(A): I'm not really sure what this is talking about.
(B): Any two different eigenstates are mutually orthogonal. So in any transition this is required.
(C): The eigenstates that are zero at the center are those with l>0. This is allowed (for example l could change from 3 to 2).
(E): The selection rules require l to change.
|
alemsalem
2010-09-21 04:32:38 |
the states with even l have even parity(1) and those with odd l have odd parity(-1) since in transitions l changes by plus or minus 1 the parity must change in any transition, so (A) is out
|
|  | lattes
2008-10-13 09:18:54 | it might be useful to make an analogy with electromagnetism. It's known that a pulsating sphere does not emit radiation because of its spherical symmetry. An analogy can be made with wave-function. (D). For further reading check out Beiser's book on modern physics pag. 165. |  | curie
2008-10-08 05:55:58 | Why does spherically-symmetric imply same angular momentum?
rkraman
2008-10-15 14:35:02 |
This has to do with the symmetry properties in mechanics. If the Lagrangian (and hence the Hamiltonian) describing a system is symmetrical with respect to any coordinate, then the canonical momentum corresponding to that coordinate is conserved. So if there is translation symmetry in  , the the canonical momentum which is the linear momentum , the the canonical momentum which is the linear momentum 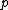 is conserved. Similarly if the Hamiltonian is rotationally invariant, it is symmetrical with respect to is conserved. Similarly if the Hamiltonian is rotationally invariant, it is symmetrical with respect to  , then the corresponding angular momentum , then the corresponding angular momentum  , which is nothing but the angular momentum , which is nothing but the angular momentum 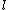 , is conserved. This is a specific instance of a fundamental theorem in Physics called the Noether's theorem. , is conserved. This is a specific instance of a fundamental theorem in Physics called the Noether's theorem.
|
spacemanERAU
2009-10-15 18:04:53 |
VERY VERY good explanation rkraman! kudos!
|
flyboy621
2010-11-14 20:52:31 |
Also, if the wavefunction is spherically symmetric, that means 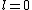 . .
|
|  | evanb
2008-06-20 11:56:30 | "completely unique relative..."
I'm not sure exactly what that means, but if it means that m must also change that's not quite right.
The selection rules are that NO TRANSITION OCCURS UNLESS:
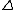 m = {-1, 0, +1} and m = {-1, 0, +1} and
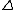 l = {-1 , +1}. l = {-1 , +1}.
 has has  ore options. ore options. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
