ernest21
2019-08-10 03:09:38 | So changing your energy from a circular orbit will give you an ellipse... increase energy too much and you can eventually reach a hyperbolic orbit. ereading games |  |
fredluis
2019-08-08 12:47:54 | You have a typo in your explanation. I\'m not the greatest speller but I think in the fourth paragraph, second sentence, it should be \"affect\" instead of \"effect\". carpet cleaner |  |
joshuaprice153
2019-08-08 04:59:24 | Hello! Someone in my Facebook group shared this website with us, so I came to give it a look. I’m enjoying the information. I’m bookmarking and will be tweeting this to my followers! Wonderful blog and amazing design and style. towing service |  |
tHulk
2012-05-19 10:45:19 | What is this equation called for  ? I can't seem to find it in any of my text books. ? I can't seem to find it in any of my text books.
tHulk
2012-05-19 11:11:20 |
Oh I see it comes from Maxwell's equations. http://en.wikipedia.org/wiki/Maxwell's_equations#With_neither_charges_nor_currents
|
|  |
livieratos
2011-11-07 07:30:34 | hmm you got me confused... i thought the speed of an em wave was always the phase velocity. what does group velocity have to do with anything? |  |
swimjk89
2010-03-21 11:31:13 | I'm not sure if I am right here, but according to (http://www.microwaves101.com/encyclopedia/phasevelocity.cfm)
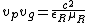
where 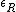 and and  are the relative permittivity and permeability. Since are the relative permittivity and permeability. Since
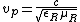
these two equations would imply for this problem that 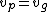 . I think that this would make sense if dealing with monochromatic light. . I think that this would make sense if dealing with monochromatic light.
swimjk89
2010-03-21 11:32:29 |
I forgot to say this means the answer would be (D)
|
|  |
rehab
2009-10-27 18:13:50 | the answer must be (B )otherwise groub velocity will exceed the speed of light from this realtion vp=c^2/vg and that ,of course, impossible!!rn
flyboy621
2010-11-09 20:07:51 |
The relation  does not always hold. does not always hold.
|
ngendler
2015-10-20 21:54:15 |
The group velocity can exceed the speed of light. Information is carried only at the phase velocity. For example, consider the following scenario: you shine a laser at the moon, and move the point to the right. If you measure the \"speed\" of the laser point, you might get a value greater than the speed of light, but that\'s okay because no new information was transmitted.
|
|  |
smokwzbroiplytowej
2008-10-22 19:18:33 | Not _exactly_ related to this problem, but Wikipedia has a nice applet showing the difference between group and phase velocity:
http://en.wikipedia.org/wiki/Group_velocity
|  |
blue_down_quark
2008-08-02 09:10:29 | I think the answer is incorrect. The question doesn't ask 'what is light's velocity ?' it instead asks 'what is light's PHASE VELOCITY? '. Phase velocity can actually be larger than c . The equation for phase velocity is 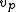 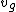 = = 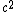 . I think the correct answer is B . for more information see : http://en.wikipedia.org/wiki/Phase_velocity . I think the correct answer is B . for more information see : http://en.wikipedia.org/wiki/Phase_velocity
wangjj0120
2008-08-20 20:59:02 |
but when is the equation v_pv_g = c^2 valid?
To integrate this equation, we realize that
only when the light propagate in the air and wave guide (or plasma) have the dispersion relation which corresponds to this equation.
|
zaijings
2009-04-03 08:22:28 |
I am also confused when the problem asks about the phase velocity.
|
segfault
2009-08-22 21:06:49 |
I think when dealing with a signal of a single frequency (e.g., blue light), it only makes sense to talk about the phase velocity--you can't construct a "group" or wavepacket out of a single frequency signal.
|
jchys
2010-02-02 20:38:17 |
If you look at the section carefully, it says that
"any particle that has MASS (according to special relativity) phase velocity of matter waves always exceeds c"
photons obviously has no mass.
|
alemsalem
2010-09-20 03:51:17 |
the refractive index is always defined in terms of v_p and it's equal to (Ke * Km)^0.5 where Ks are the relative permittivity and permeability.
|
misbah
2014-12-05 02:13:46 |
i agree with kittle 's book view
|
|  |
erc
2005-11-04 09:11:07 | I don\'t know anything about this, so maybe about to make a fool of myself...
But, to be consistent, I think the 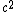 and and 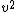 should each lose the power? should each lose the power?
Thanks.
yosun
2005-11-04 15:10:14 |
erc: thanks for the typo note. The extra squared sign on the c's and v's have been removed. (you can also check it by dimensional analysis. the units for permeability and permittivity are given on the table of info included with the exam)
|
|  |
erc
2005-11-04 09:09:06 |
rehab
2009-10-27 18:30:09 |
the answer must be (B )otherwise groub velocity will exceed the speed of light from this realtion vp=c^2/vg and that ,of cource, impossible!!
|
|  |
