toto212
2019-11-16 05:06:24 | Hello , i Just want to say that, umm..\\\\r\\\\nwhat u make is very amazing and i also like it ^.^\\\\r\\\\nThanks friend. I hope i can see your various works.\\\\r\\\\nKeep working guys. jayatogel " target="_blank">http://68.65.120.68/situs-resmi-togel-online-jayatogel/\\\\\\\">jayatogel |  |
ernest21
2019-08-10 03:09:48 | Your solution stills showing the area proportional to d^(2*ne). Although, it is not to worry. progressive rummy |  |
fredluis
2019-08-08 12:31:01 | I will must share this blog and the information i found here really has no value in money but more than it. Thanks for this nice effort which you put here in the shape of this post. carpet cleaner |  |
joshuaprice153
2019-08-08 06:17:59 | A perfect info source. Thanks for taking the time to discuss this, I feel strongly about it and love learning more on this topic. house painting |  |
casseverhart13
2019-08-02 11:03:15 | I just added this web site to my feed reader, excellent problem. tree pruning |  |
jonny77
2018-05-25 12:47:30 | Ahaa, its nice conversation about this piece of writing here at this blog, I have read all that, so now me also commenting at this place.\r\n\r\n http://www.masteragen.top/ taruhan judi bola \r\n http://masteragen.xyz/ sepak bola dunia terkini \r\n http://blog.masteragen.top/category/prediksi-pertandingan/ prediksi piala eropa hari ini |  |
jonny77
2018-05-25 12:47:16 | Ahaa, its nice conversation about this post here at this blog, I have read all that, so now me also commenting at this place.\r\n\r\n http://anakgawang.com/ Berita Ronaldo \r\n http://livescorebolas.com/ Read More \r\n http://indobola.me/ tebak skor bola |  |
jonny77
2018-05-25 12:47:07 | I couldn\'t resist commenting. Perfectly written!\r\n\r\n http://medikapedia.com/ selengkapnya \r\n http://servicewikawaterheater.com Telepon Service Wika |  |
jonny77
2018-05-25 12:46:44 | I\'ve been browsing online more than three hours today, yet I never found any interesting article like yours. It is pretty worth enough for me. In my view, if all web owners and bloggers made good content as you did, the web will be much more useful than ever before.\r\n\r\n http://jmbnm.com/daftar-5-pencapaian-rekor-yang-belum-terpecahkan-oleh-cristiano-ronaldo/ web judi online terpercaya \r\n http://gcchrshare.com/deretan-pemain-liga-inggris-yang-berpenghasilan-kurang-dari-10-ribu-pounds-per-minggu/ akun bola online \r\n http://lamassupro.com/4-bomber-berkelas-yang-hanya-menjadi-cadangan/ agen ibcbet terpercaya \r\n http://shbae.com/4-bintang-liverpool-yang-di-jual-dalam-6-tahun-terakhir/ sboagen \r\n http://ifrb.info/3-pelatih-yang-dikabarkan-akan-dipecat-klubnya-musim-panas-nanti/ judi casino |  |
NAJUM UDDIN
2017-01-20 04:49:49 | THANKS \r\n |  |
varshakr
2016-12-27 10:46:29 | depends on units |  |
Giubenez
2014-10-22 02:55:55 | Nice bad pics:
the trend for x>R isn't an inverse square (if you estimate for E(x=2R)/E(R) you find 1/2 and not 1/4.
Furthermore it seems to have an horizontal asymptote > 0......
And so, all the graph are wrong. |  |
flyboy621
2010-11-09 20:54:39 | A minor correction: the field increases linearly with the radius of the sphere, not the volume. Hence the straight line of graph C.
funnyjokes
2018-04-12 01:48:26 |
Thanks for your sharing. http://tellfunnyjokes.com Hope you can contribute more quality posts to this page. Thank you!\r\n
|
|  |
nmast
2009-11-24 09:16:37 | Since the charge density is uniform, shouldn't E go like Q enclosed? Being a sphere, this would be like r^3, making D correct.
kroner
2009-11-27 19:08:54 |
No. Q is proportional to 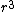 , but E is proportional to , but E is proportional to 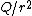 which means E is linear in r, as in choice C. which means E is linear in r, as in choice C.
|
|  |
wittensdog
2009-09-24 21:45:16 | ETS sure does love to throw in unnecessary details - who cares if the charge is positive or negative when it comes to the field magnitude? |  |
Andresito
2006-03-14 22:37:41 | Gauss' law E*A = Q/epsilon
Yours is an approximation.
Thanks Yosun.
lxanderl
2009-06-28 17:23:43 |
Depends on if he's using cgs or SI
|
|  |
