|
GR8677 #9
|
|
|
|
|
Alternate Solutions |
thinkexist
2012-10-12 14:37:10 | You can solve this by common sense and a little physics.
Firstly, it doesn't make much sense for an electron to be traveling speeds comparable to the size of a proton per second. Exclude A, B, C.
You also know that current works by the propagation of the coulomb force so when you put one electron into a filled tube of electrons a different electron on the other side of the tube pops out because of the coulomb force. Having said that, it doesn't really make much sense for the electron to be traveling 10^3 m/s when there are a ton of electrons it can bounce into including the atoms. Exclude E.
What we have left is D. |  | flyboy621
2010-11-09 20:51:08 | 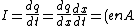(v_d)) , ,
where  is the electron charge, is the electron charge,  is the electron density, is the electron density, 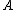 is the cross-sectional area of the wire, and is the cross-sectional area of the wire, and 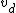 is the drift velocity. is the drift velocity.
Solve for 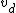 , plug in rough numbers, and you get: , plug in rough numbers, and you get:
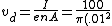(10^{28})(1.6\times10^{-19})}\approx\frac{10^{-3}}{5}=2\times10^{-4}) , which matches (D). , which matches (D). |  | Ben
2005-12-01 13:23:38 | I did it using unit analysis sort of. Boils down to the same thing but I get much closer to 2E-4.
100A = 100 C/s
(100 C/s)*(1/1.6E-19 e-/C) = 6.25E20 e-/s
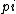 r^2 = r^2 = 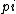 E-4 E-4
(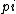 E-4 m^2)*(1E28 e-/m^3) = E-4 m^2)*(1E28 e-/m^3) = 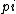 E24 e-/m (of wire) E24 e-/m (of wire)
Finally:
(6.25E20 e-/s)*(1/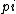 E24 m/e-) which gives pretty close to 2E-4 E24 m/e-) which gives pretty close to 2E-4
(hopefully my latex pi's worked) |  |
|
|
Comments |
ernest21
2019-08-10 03:09:47 | I think m was mass not meter, otherwise it made no sense at all. strategy gamer |  | joshuaprice153
2019-08-08 06:10:59 | Thanks for taking this opportunity to discuss this, I feel fervently about this and I like learning about this subject. event planner Orlando |  | thinkexist
2012-10-12 14:37:10 | You can solve this by common sense and a little physics.
Firstly, it doesn't make much sense for an electron to be traveling speeds comparable to the size of a proton per second. Exclude A, B, C.
You also know that current works by the propagation of the coulomb force so when you put one electron into a filled tube of electrons a different electron on the other side of the tube pops out because of the coulomb force. Having said that, it doesn't really make much sense for the electron to be traveling 10^3 m/s when there are a ton of electrons it can bounce into including the atoms. Exclude E.
What we have left is D. |  | natestree
2011-03-22 14:47:19 | So, I figured the correct answer w/o any knownledge on drift velocity and some simple unit analysis.
Note the units for quantities given.
current is charge per time.
diameter is meters
density is # of particle per cubic meter
we want something in units of meters per second. Therefor, we can use the quantities given to come up with the relation:
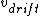 = = 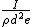
Where I is current,  is the density, e is charge of an electron, and d is the diameter. This gives an answer ~ is the density, e is charge of an electron, and d is the diameter. This gives an answer ~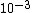 which is closest to option D. which is closest to option D. |  | flyboy621
2010-11-09 20:51:08 | 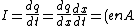(v_d)) , ,
where  is the electron charge, is the electron charge,  is the electron density, is the electron density, 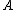 is the cross-sectional area of the wire, and is the cross-sectional area of the wire, and 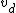 is the drift velocity. is the drift velocity.
Solve for 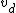 , plug in rough numbers, and you get: , plug in rough numbers, and you get:
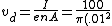(10^{28})(1.6\times10^{-19})}\approx\frac{10^{-3}}{5}=2\times10^{-4}) , which matches (D). , which matches (D).
walczyk
2011-04-06 16:27:46 |
this is by far the best way to do this. its perfect when you can derive it so quickly and easily like that, i just wish i recognized it too. forget all the equations. follow this. intuition is our friend
|
|  | kicksp
2007-10-29 09:42:47 | Inspection shows that the choices are separated by several orders of magnitude. Hence, we need only an order of magnitude estimate:
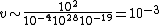
The answer is clearly (D). Throw in the factor 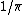 and you obtain and you obtain 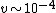 . .
Go maroons! |  | Andresito
2006-03-14 22:16:53 | Your solution stills showing the area proportional to d^(2*ne). Although, it is not to worry.
thanks Yosun.
Andresito
2006-03-14 22:18:21 |
"Nevermind"
|
|  | wishIwasaphysicist
2006-01-24 11:22:51 | oops...you were right. I took the diamter squared and not radius squared. It comes out to 2 E -4 m/s and not 3 E - 4 m/s though. |  | wishIwasaphysicist
2006-01-24 11:08:34 | I don't see where the 4 in front of current (I) came from. If you remove it, you get exactly the answer choice: 2 E -4 m/s.
grae313
2007-10-07 15:11:30 |
It comes from squaring the radius (d/2) to get the cross sectional area
|
|  | Ben
2005-12-01 13:23:38 | I did it using unit analysis sort of. Boils down to the same thing but I get much closer to 2E-4.
100A = 100 C/s
(100 C/s)*(1/1.6E-19 e-/C) = 6.25E20 e-/s
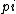 r^2 = r^2 = 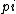 E-4 E-4
(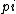 E-4 m^2)*(1E28 e-/m^3) = E-4 m^2)*(1E28 e-/m^3) = 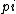 E24 e-/m (of wire) E24 e-/m (of wire)
Finally:
(6.25E20 e-/s)*(1/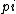 E24 m/e-) which gives pretty close to 2E-4 E24 m/e-) which gives pretty close to 2E-4
(hopefully my latex pi's worked)
yosun
2005-12-02 01:10:35 |
ben: your LaTeX came out iffy. you should have used a \ (back-slash) sign before your pi's (and other latex commands) so that you type-set  instead of instead of  . it's been manually corrected. . it's been manually corrected.
(for everyone else with typos i didn't get to catch: over winter break, i'd code options for edit-posts, among other features.)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
