|
GR0177 #99
|
|
|
Problem
|
|
|
This problem is still being typed. |
Special Relativity }Conservation of Energy }Conservation of Energy
The tricky part of this problem is to note that the momentum of the photon is shared equally between all three final particles. (This insight was supplied by Felipe Birk). Thus, 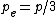 , where p is the momentum of the photon and , where p is the momentum of the photon and 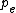 is the momentum of the final electron or photon. is the momentum of the final electron or photon.
The initial energy before the photon strikes the electron is 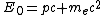 , which is just the energy of the photon plus the rest energy of the electron. , which is just the energy of the photon plus the rest energy of the electron.
The final energy after the collision is ^2+(m_e c^2)}) , which is the sum total energy of all three final particles, i.e., the positron and two electrons. (A positron is the electron's antiparticle, and thus they have the same mass.) Note that the momentum split relation mentioned above is used to equate the final particle momentum with the initial photon momentum. , which is the sum total energy of all three final particles, i.e., the positron and two electrons. (A positron is the electron's antiparticle, and thus they have the same mass.) Note that the momentum split relation mentioned above is used to equate the final particle momentum with the initial photon momentum.
Conjure up the good conservation of energy idea. Equating 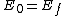 , one gets , one gets ^2+(m_ec^2)^2 + 2pcm_ec^2 = 9((pc/3)^2+(m_ec^2)^2)) . Canceling the . Canceling the ^2) terms on both side, then solving, one arrives at terms on both side, then solving, one arrives at 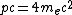 , which is choice (D). , which is choice (D). |
|
|
Alternate Solutions |
opalqnka
2014-10-15 01:29:53 | You all post nasty solutions.
Here is an easy one:
The 4-momentum of the photon in the lab frame and the 4-momentum of the stationary electron are:
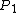 = =) and and  = =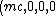)
After the interaction 3 particles of equal masses and equal energies and momenta are created with the same 4-momentum vector of 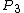 . We do not care about the form of the . We do not care about the form of the 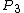 momentum, you will see why below: momentum, you will see why below:
Use conservation of 4-momenta:
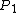 + +  = 3 = 3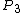
Now square (using the dot product with [-, +, +, +] metric) and use the fact that for a photon P.P = 0 and in the rest frame of the electrons/protons  . . = = 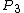 . .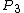 = - = - 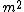 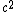 , ie we exploit the fact that P.P is invariant! , ie we exploit the fact that P.P is invariant!
=>
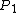 . .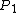 + 2 + 2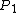 . . + +  . . = 9 = 9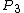 . .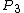
or
0 - 2Em - 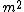 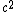 = -9 = -9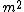 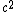
or E = 4m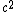 as in answer (D). as in answer (D).
I hope you will find this approach useful. Thank you for hosting the site! |  | ArslanUyghur
2014-09-25 03:50:08 | No four vectors and any frames, you can use just Energy–momentum relation and Energy and momentum conservation law:
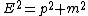 (basic equation) (basic equation)
for the photon we have:
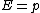 (remember its mass is zero) (remember its mass is zero)
for the electron before collision
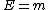 (here p=0) (here p=0)
so the total energy of the system before collision is:
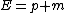
or
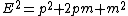
Now let's see what is the energy of the system after collision, using Energy–momentum relation we get:
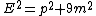
where p is the same momentum of the photon or total linear momentum of three particles(since momentum is conserved).
Equating the two expressions for square of energy, we obtain the following:
 =p^2+9m^2$ =p^2+9m^2$
The solution is:
p=4m
or in SI units:
p=4mc
and energy of the photon is 4mc^2.
The answer is D. |  | vadim
2012-11-08 12:52:15 | Shorter solution using relativistic invariant:
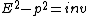
Comparing this value in initial laboratory frame and in final frame of particles one can obtain:
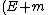^2-p^2=(3m)^2)
As far as photon is concerned,  , which brings us to , which brings us to 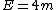 , or in SI , or in SI  |  | insertphyspun
2011-06-26 12:13:41 | I have not yet seen the simplest solution, although dryu and matonski came close. Yes, you should use four vectors, but recall that the square of the momentum four vector is invariant! So, jump into the CM reference frame when determining the momentum four vector after the collision to make life simpler! To be more explicit, here it goes:
The momentum four vector before the collision, where 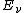 is the energy of the incoming photon and is the energy of the incoming photon and 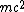 is the rest energy of the electron, is is the rest energy of the electron, is
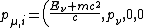)
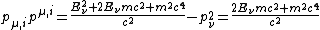
(Using 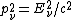 should be second nature by now!) should be second nature by now!)
The momentum four vector after the collision, taken in the CM frame of the three particles, is awesomely simple,
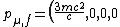)

The squared four vectors are equal, so put them together and solve for 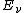 ! !
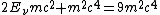
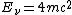 |  | dryu
2008-10-17 22:32:47 | It's simplest to use four vectors. In natural units:
The initial four-momentum is ) and the final four-momentum is and the final four-momentum is ) . The invariant mass, e.g. these four vectors squared, is conserved: . The invariant mass, e.g. these four vectors squared, is conserved:
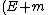^2-E^2=9(\gamma^2m^2-\gamma^2m^2v^2))
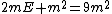
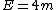
To convert this into SI units, just let 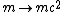 . . |  |
|
|
Comments |
opalqnka
2014-10-15 01:29:53 | You all post nasty solutions.
Here is an easy one:
The 4-momentum of the photon in the lab frame and the 4-momentum of the stationary electron are:
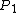 = =) and and  = =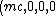)
After the interaction 3 particles of equal masses and equal energies and momenta are created with the same 4-momentum vector of 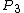 . We do not care about the form of the . We do not care about the form of the 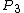 momentum, you will see why below: momentum, you will see why below:
Use conservation of 4-momenta:
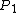 + +  = 3 = 3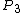
Now square (using the dot product with [-, +, +, +] metric) and use the fact that for a photon P.P = 0 and in the rest frame of the electrons/protons  . . = = 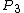 . .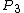 = - = - 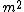 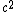 , ie we exploit the fact that P.P is invariant! , ie we exploit the fact that P.P is invariant!
=>
 . . + 2 + 2 . . + +  . . = 9 = 9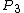 . .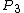
or
0 - 2Em - 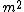 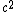 = -9 = -9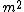 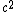
or E = 4m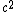 as in answer (D). as in answer (D).
I hope you will find this approach useful. Thank you for hosting the site!
shka
2018-07-09 17:59:48 |
*reads Yohni Kahn once* *becomes Einstein*
|
shka
2018-07-09 18:02:05 |
nice typo btw
|
|  | opalqnka
2014-10-15 01:24:54 | You all post nasty solutions.
Here is an easy one:
The 4-momentum of the photon in the lab frabe and the 4-momentum of the stationary electron are:
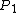 = =) and and  = =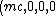)
After the interaction 3 particles of equal masses and equal energies and momenta are created with the same 4-momentum vector of 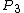 . We do not care about the form of the . We do not care about the form of the 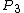 momentum, you will see why below: momentum, you will see why below:
Use conservation of 4-momenta:
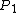 + +  = 3 = 3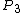
Now square (using the dot product with [-, +, +, +] metric) and use the fact that for a photon P.P = 0 and in the rest frame of the electrons/protons  . . = = 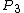 . .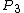 = - = - 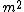 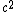 , ie we exploit the fact that P.P is invariant! , ie we exploit the fact that P.P is invariant!
=>
 . . + 2 + 2 . . + +  . . = 9 = 9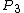 . .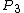
or
0 - 2Em - 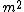 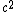 = -9 = -9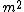 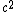
or E = 4m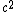 as in answer (D). as in answer (D).
I hope you will find this approach useful. Thank you for hosting the site!
|  | ArslanUyghur
2014-09-25 03:50:08 | No four vectors and any frames, you can use just Energy–momentum relation and Energy and momentum conservation law:
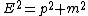 (basic equation) (basic equation)
for the photon we have:
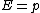 (remember its mass is zero) (remember its mass is zero)
for the electron before collision
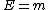 (here p=0) (here p=0)
so the total energy of the system before collision is:
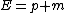
or
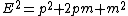
Now let's see what is the energy of the system after collision, using Energy–momentum relation we get:
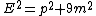
where p is the same momentum of the photon or total linear momentum of three particles(since momentum is conserved).
Equating the two expressions for square of energy, we obtain the following:
 =p^2+9m^2$ =p^2+9m^2$
The solution is:
p=4m
or in SI units:
p=4mc
and energy of the photon is 4mc^2.
The answer is D.
JM777
2018-08-06 07:07:27 |
Nice job!
|
|  | sayebms
2013-09-01 02:28:08 | first of all thank you for such a great website.
in this problem we apply both conservation of momentum and conservation of energy.(since we have two unknowns we must have two equations)
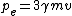 call call 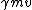 as as 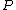 which is the individual momentum for each particle. which is the individual momentum for each particle.
then
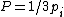
now apply conservation of energy as given in the solution above. |  | vadim
2012-11-08 12:52:15 | Shorter solution using relativistic invariant:
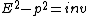
Comparing this value in initial laboratory frame and in final frame of particles one can obtain:
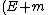^2-p^2=(3m)^2)
As far as photon is concerned,  , which brings us to , which brings us to 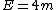 , or in SI , or in SI  |  | insertphyspun
2011-06-26 12:13:41 | I have not yet seen the simplest solution, although dryu and matonski came close. Yes, you should use four vectors, but recall that the square of the momentum four vector is invariant! So, jump into the CM reference frame when determining the momentum four vector after the collision to make life simpler! To be more explicit, here it goes:
The momentum four vector before the collision, where 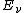 is the energy of the incoming photon and is the energy of the incoming photon and 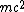 is the rest energy of the electron, is is the rest energy of the electron, is
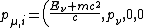)
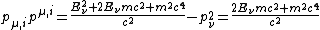
(Using 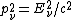 should be second nature by now!) should be second nature by now!)
The momentum four vector after the collision, taken in the CM frame of the three particles, is awesomely simple,
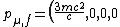)

The squared four vectors are equal, so put them together and solve for 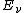 ! !
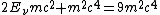
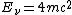
4elesta
2012-04-16 06:11:25 |
Don't understand why initial energy of photon doesn't change in the rest reference frame?
|
walczyk
2012-11-05 19:11:32 |
It does change, it is not lorentz invariant. Doesn't matter, because only lorentz invariant quantities are independent of reference frame, we are not dealing with energy directly here, only where it turns up in the momentum four-vector elements.
|
|  | erica1989
2010-11-08 21:13:20 | Sorry about the multipost, was having issues with the browser. |  | astro8
2010-09-14 21:09:46 | The only part i am confused on is  not being a square root of the squares. not being a square root of the squares.
ie. 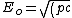^2 + \left(m_ec^2\right)^2})
Is this form of the total energy only used for multiple kinetic and potential energies being added?
tiptoer
2010-10-26 08:32:07 |
I have the same question. Why is  instead of instead of 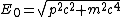 ? ?
|
aqme28
2010-11-09 18:52:58 |
I was confused about this at first too, but I figured it out. Yosun just skipped a few steps algebraically.
^2) since a photon has no mass since a photon has no mass
^2) since the electron is initially at rest and therefore momentum is 0. since the electron is initially at rest and therefore momentum is 0.
so 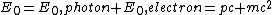
|
|  | zmburell
2009-09-30 13:05:08 | The electron is inititially at rest, so in the expression for the initial 4-momentum squared, why isnt (pc)=0,
That is, if the electron is initially at rest then all of its energy is in its rest mass
zmburell
2009-10-03 10:36:56 |
Nevermind, Im retarded, I figured it out
disregard my last post
|
|  | matonski
2009-04-01 00:35:29 | In a reference frame moving along with the three particles at the end, the magnitude of the momentum 4 vector is simply 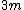 . Since this is an invariant, it must also be the magnitude of the 4 vector at the beginning. Letting . Since this is an invariant, it must also be the magnitude of the 4 vector at the beginning. Letting  be the initial photon energy and setting be the initial photon energy and setting 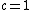 , we have , we have ^2) and and 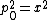 . Therefore, its magnitude is . Therefore, its magnitude is ^2 = (m+x)^2 - x^2) Solve for x and you are done. Solve for x and you are done. |  | Poop Loops
2008-11-02 14:41:44 | I'm confused... if they don't say how fast the 3 particles are moving, how can we deduce the energy of the photon? It was at least 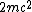 since it created a positron and an electron and then moved them. Okay, that makes sense. since it created a positron and an electron and then moved them. Okay, that makes sense.
But if the collision sent all 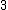 going at going at 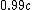 then the photon would have had more energy than if they were all going at say then the photon would have had more energy than if they were all going at say 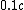 afterwards. What gives? afterwards. What gives?
flyboy621
2010-11-16 22:12:32 |
Conservation of momentum requires the 3 particles to have total momentum equal to the momentum of the photon. We are given that they have equal speeds, so they each have momentum 1/3 that of the photon.
|
|  | dryu
2008-10-17 22:32:47 | It's simplest to use four vectors. In natural units:
The initial four-momentum is ) and the final four-momentum is and the final four-momentum is ) . The invariant mass, e.g. these four vectors squared, is conserved: . The invariant mass, e.g. these four vectors squared, is conserved:
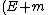^2-E^2=9(\gamma^2m^2-\gamma^2m^2v^2))
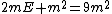
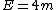
To convert this into SI units, just let 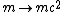 . .
cbb6x2
2010-11-04 10:35:19 |
E0=Ef where E0 is the total energy before and Ef is the total energy after. The total energy is the energy of each particle summed. Find the energy of each particle separately where (E_particle)^2 = (pc)^2+(mc^2)^2.
E0=E_gamma + E_electron=(pc)^2 +mc^2
|
erica1989
2010-11-08 21:09:34 |
Can you please explain how you got the expression for the four vectors? Thanks!
|
erica1989
2010-11-08 21:10:32 |
Hi
Can you please explain how you got the expression for the four vectors? Thanks!
|
erica1989
2010-11-08 21:12:07 |
Hi can you please explain how you got this expression?
|
neo55378008
2012-03-20 21:10:51 |
It's a shame most books don't teach four-vectors until GR.
Basically, the first component of four-momentum is the energy (as a particle moves through time it has energy), and the other components are just the x, y, and z components of momentum.
The to four-vectors is the metric. For SR you can use (+---) or (-+++) as long as you're consistent.
dryu has used the (+---) metric, meaning when you take a dot product, the time components keep their sign, and the space components get the opposite sign.
|
neo55378008
2012-03-20 21:11:43 |
*they key to the four-vector is the metric
|
|  | ssp
2008-10-17 12:35:10 | Why does not common sense work?rnrnYou create 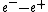 pair, that is an energy of pair, that is an energy of 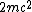 rnYou put energy into the resting rnYou put energy into the resting 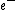 that gets some energy that gets some energy 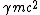 rnThen you need energy to make the rnThen you need energy to make the 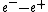 pair move, so you need pair move, so you need 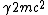 for the total energy of those particles.rnrnAdding up all energy you need to get something above 3 at least... you are down to 2 answers and 5 seems a bit large for for the total energy of those particles.rnrnAdding up all energy you need to get something above 3 at least... you are down to 2 answers and 5 seems a bit large for 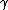 so you pick 4 so you pick 4
physick
2011-09-25 10:16:05 |
This approach works fine -- as you said, the answer must be over 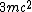 , which narrows it down to D and E. Then use the fact that there is an upper limit on the amount of energy the photon could have (such that the speed of the particles doesn't exceed , which narrows it down to D and E. Then use the fact that there is an upper limit on the amount of energy the photon could have (such that the speed of the particles doesn't exceed  ). This means that if E is possible, then D would have to be possible too! Since the reverse is not true, we may eliminate E to select D as the answer. ). This means that if E is possible, then D would have to be possible too! Since the reverse is not true, we may eliminate E to select D as the answer.
This method eliminates option E a bit more logically instead of leaving it to the sense that E "seems a bit large."
|
|  | Ning Bao
2008-02-01 08:26:25 | If we set c and m=1 and let p=a*m=a The math becomes much simpler. |  | Tommy Koulax
2007-11-01 22:08:02 | I don't understand why p is divided by three. If the photon is no longer, then shouldn't the p be divided by 2?
alpha
2008-02-07 11:02:47 |
i think it is because there are 3 final particles?
|
|  | TigerTed8
2007-09-13 18:14:56 | Although the overall solution seems okay, I think there is a small typo. ^2+(m_e c^2)^2}) . Note the second squared on the second term. . Note the second squared on the second term.
sravani
2008-10-09 19:05:48 |
TigerTed8 is right. Solution has to be corrected by squaring the second term. Yosun, you got to correct it...
|
zylstra
2009-04-01 18:35:24 |
Please excuse my ignorance. How did you get this formula for 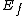 ? ?
|
|  | angiep
2005-11-11 22:17:50 | im confused, the problem says the photon is destroyed. you say all three share the momtentum, but there are only 2...
angiep
2005-11-11 22:18:29 |
nevermind. two electrons, duh
|
|  | Void
2005-11-09 23:08:19 | Hi Yosun. Great site. I have a few solutions to GR9677 that aren't on your PDF yet. Do you take submissions? How should I send them, if so?
yosun
2005-11-09 23:36:54 |
Hi, please post alternate solutions on the website in the comments section corresponding to the particular problem. (The pdf I posted in the yahoo physicsgre group is incomplete and contains a number of errors that I have corrected here on this site. Of course, users like you might have more elegant solutions than what I have posted---so, feel free to post away. This site aims to be the most convenient one-stop source for all solutions to released ETS GRE Physics exams. You can help by contributing.)
|
|  | yosun
2005-11-09 22:08:33 | This solution has been corrected. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
