|
GR0177 #96
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Symmetry }Symmetry
By symmetry, the total power radiated is 0. It expands inwards and outwards at the same frequency.
|
|
|
Alternate Solutions |
sigma
2013-10-18 15:58:50 | The important thing to note here is that in order to have radiation, you need to have a magnetic field.
Which direction would that magnetic field point if one was to exist? (this is the symmetry argument)
Griffiths's argument as above is crap, because Gauss's law only holds for electrostatics and precisely excludes radiation. That is to say, when you are more precise in solving Maxwell's equations for the fields, you get terms that are dependent ONLY on the configuration at each time (these are spooky terms where signals propagate instantaneously -- Gauss's law and Biot-Savart) and then you get dynamical terms which precisely cancel the spooky ones and give you the interesting, time-dependent part.
symmetry -> magnetic field is zero -> no radiation |  | torturedbabycow
2010-04-06 11:33:22 | A fact I memorized about radiation for a small oscillating charge came in useful for me here:
There is NO radiation along the axis of oscillation. For a uniformly expanding/contracting sphere, the "axis of oscillation" is radial, so there is no radiation at all! (Of course, this does assume that if there is radiation, it has to be in the radial direction, which makes sense based on symmetry.)
Completely non-rigorous, I know, but these two facts are useful mnemonics for each other for me. |  | mitama
2008-08-10 11:42:47 | I agree that the electric field remains constant, but shouldn't the magnetic field be accounted for as well? The total power would be calculated using a surface integral of the Poynting vector, which depends on both the electric and magnetic fields. rnrnMy approach was to break the problem down into an infinite number of 1D problems, where you have a single charge oscillating along a radial line. We know in this case, there is no radiation along the line of oscillation, so there is no power output radially out. The EM radiation, off the line of oscillation, would just cancel with the radiation from neighboring charges. This makes sense, since from rotational symmetry of the sphere, there can only be radial dependence. |  | sblusk
2006-10-25 08:30:50 | Perhaps it is worth being more clear here. Using symmetry and Gauss's Law, the electric field is proportional to the charge inside a Gaussian sphere. Since the contained charge does not change, the electric field does not change, and therefore there is no monopole radiation. Also, by symmetry the dipole moment is zero for a unifromly charged sphere, so dp/dt=0, and hence no dipole radiation. Similarly, the higher multipoles are also zero. |  |
|
|
Comments |
sigma
2013-10-18 15:58:50 | The important thing to note here is that in order to have radiation, you need to have a magnetic field.
Which direction would that magnetic field point if one was to exist? (this is the symmetry argument)
Griffiths's argument as above is crap, because Gauss's law only holds for electrostatics and precisely excludes radiation. That is to say, when you are more precise in solving Maxwell's equations for the fields, you get terms that are dependent ONLY on the configuration at each time (these are spooky terms where signals propagate instantaneously -- Gauss's law and Biot-Savart) and then you get dynamical terms which precisely cancel the spooky ones and give you the interesting, time-dependent part.
symmetry -> magnetic field is zero -> no radiation
HYaorUan
2016-04-12 15:01:18 |
you did not even quote which page which line.
|
kronotsky
2018-10-25 02:57:36 |
I\'m sorry, but you are misinformed about Gauss\'s law. Classically, Maxwell\'s equations hold at any instant in a given frame. Gauss\'s law simply follows from the divergence theorem and the first equation. It may even be more appropriate to say that the first equation is Gauss\'s law. Gauss\'s law certainly applies for radiated fields (and causal propagation fields traveling at the speed of light), though radiation typically breaks the electrostatic symmetry. But in this case, the symmetry argument you use to apply the integral form of Gauss\'s law has exactly the same content as the symmetry argument you use to exclude radiation.
|
|  | gamercora
2010-09-07 08:31:58 | I thought of Larmor formula too. considering the frequency f, the acceleration is proportional to f^2,so the power is proportional to f^4. But in the region of R>R2, according to Guass law the electromagnetic field is constant and there is no radiation loss. power change only happenes in the region of RReply to this comment |  | torturedbabycow
2010-04-06 11:33:22 | A fact I memorized about radiation for a small oscillating charge came in useful for me here:
There is NO radiation along the axis of oscillation. For a uniformly expanding/contracting sphere, the "axis of oscillation" is radial, so there is no radiation at all! (Of course, this does assume that if there is radiation, it has to be in the radial direction, which makes sense based on symmetry.)
Completely non-rigorous, I know, but these two facts are useful mnemonics for each other for me. |  | tsharky87
2009-11-06 23:08:30 | I made the very quick assumption that the sphere was known to be radiating, not because of the oscillations, but because it was accelerating through space. So I thought of Larmor's law and deduced that the power should be proportional to Q^2, which was close enough to (A) for me. It doesn't state that it's NOT accelerating...
gamercora
2010-09-07 08:28:08 |
I thought of Larmor formula too. considering the frequency f, the acceleration is proportional to f^2,so the power is proportional to f^4. But in the region of R>R2, according to Guass law the electromagnetic field is constant and there is no radiation loss. power change only happenes in the region of R |
|  | nyuko
2009-11-05 23:27:47 | I remember a lecture of EM course I took. When the professor taught about radiation due to acceleration of electric charge, he said it is because the E-field is changing in such a way that the nature cannot interpolate (extrapolate, whatever) the new E-field. That's why electric charge moving in constant velocity does not radiate, because the nature can "interpolate" the field in the whole space at one time! For this question, the E-field in the space just does not change at all; there is no radiation. |  | cag51
2009-10-08 22:44:23 | I'm a little confused. Say you pick your Gaussian Surface in the region of fluctuation, as Richard says. Then, there are (infinitesimal) point charges that acceleration (fluctuation obey's Hooke's law), and those will emit radiation. As it contracts, it will again emit radiation, but since the new radiation is out of phase with the old radiation, the two cancel out -- so there's no disturbance to the E-field at R > R2, as is obvious. This explains everything -- the contracting radiation cancels with the expanding radiation so there's no field change at large R, and it explains how the field changes in the region of fluctuation. The problem is you can't emit "negative power" so the powers can't "cancel." What's the best way to answer the question "what's the e-field in the region of fluctuation?" |  | dstahlke
2009-10-07 11:30:11 | Due to rotational symmetry about any given axis, it is clear that both E and B must always point in the radial direction. Their cross product must then be zero and therefore the Poynting vector is everywhere zero at all times.
luftbahnfahrer
2011-10-25 07:43:46 |
This explanation really helped! Although, since the E-field is constant outside of the sphere, there wouldn't even be any B-field at all. So B is zero everywhere, and thus no Poynting vector.
|
|  | blue_down_quark
2008-09-14 00:49:11 | I solved the problem through symmetry as well. But i still wonder what happens to the oscillating field in the region 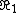 < R < < R < 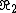 |  | mitama
2008-08-10 11:42:47 | I agree that the electric field remains constant, but shouldn't the magnetic field be accounted for as well? The total power would be calculated using a surface integral of the Poynting vector, which depends on both the electric and magnetic fields. rnrnMy approach was to break the problem down into an infinite number of 1D problems, where you have a single charge oscillating along a radial line. We know in this case, there is no radiation along the line of oscillation, so there is no power output radially out. The EM radiation, off the line of oscillation, would just cancel with the radiation from neighboring charges. This makes sense, since from rotational symmetry of the sphere, there can only be radial dependence.
aqme28
2010-11-09 18:37:46 |
but where is the magnetic field coming from? E isn't changing and there's no magnetic field to begin with.
so Ex0=0
|
|  | Richard
2007-10-30 20:32:27 | I remembered talking about this in my second semester senior E&M class. Indeed, in Griffith's book there is this statement on page 458:
You might think that a charged sphere whose radius oscillates in and out would radiate, but [then you would be a complete MORON!]---the field outside, according to Gauss's law, is exactly \hat{r}) , regardless of the fluctuations in size. , regardless of the fluctuations in size.
Okay, well the idea is that an electric 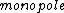 does not radiate does not radiate 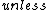 charge is not conserved. Now it seems pretty obvious to me that the TOTAL power radiated by the oscillating sphere is zero. But is there really charge is not conserved. Now it seems pretty obvious to me that the TOTAL power radiated by the oscillating sphere is zero. But is there really 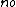 power radiated as some people have suggested? What if you choose your Gaussian surface in the region of fluctuating charge? Then charge is only conserved over a period, and power power radiated as some people have suggested? What if you choose your Gaussian surface in the region of fluctuating charge? Then charge is only conserved over a period, and power 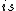 "radiated" but without really getting anywhere. "radiated" but without really getting anywhere.
|  | scottopoly
2006-11-02 21:28:18 | I agree with sblusk. In fact, I think the solution may be misguided in suggesting that there is some power radiated at some time, but it is compensated at other times, or something. It doesn't matter how the sphere expands and contracts, in any frequency at any time, as long as it's still a sphere, the E field outside it is constant. |  | sblusk
2006-10-25 08:30:50 | Perhaps it is worth being more clear here. Using symmetry and Gauss's Law, the electric field is proportional to the charge inside a Gaussian sphere. Since the contained charge does not change, the electric field does not change, and therefore there is no monopole radiation. Also, by symmetry the dipole moment is zero for a unifromly charged sphere, so dp/dt=0, and hence no dipole radiation. Similarly, the higher multipoles are also zero. |  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
