|
GR0177 #93
|
|
|
|
|
Alternate Solutions |
radicaltyro
2006-10-28 23:38:14 | One can also note that this is more or less the definition of the bohr radius. |  |
|
|
Comments |
UNKNOWNUMBER
2018-10-20 23:28:34 | I think this is one of those problems ETS expects you to know the answer to by heart after taking a quantum class. |  | bhaynor
2009-10-03 12:30:22 | I get C. It asks for the most probable value of r, not the expectation value of r. The most probable value of r occurs when Psi is maximized, at r = 0.
bhaynor
2009-10-03 12:32:07 |
Ignore my last comment. I forgot about r^2.
|
|  | anmuhich
2009-03-17 13:09:47 | You can also remember that in general lower energy states are more probable and that the lowest energy state of hydrogen is the ground state at the bohr radius. |  | Imperate
2008-10-04 14:52:04 | An interesting note on this question, is that the most probable value of r for the ground state wavefunction, is NOT equal to the expectation value.rnrnThe expectation value is actually 1.5a_o.rnrnhttp://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydr.html#c3rnrnshows nice solutions to both of these related problemsrnrn |  | radicaltyro
2006-10-28 23:38:14 | One can also note that this is more or less the definition of the bohr radius.
mitama
2008-08-09 17:56:58 |
Depending on the wavefunction, this may or may not be true (luckily, in this case it is). It's probably best to go through the work just to be sure.
|
syrock
2009-10-08 16:50:41 |
yeah, hydrogen.... bohr.... come on its gatta be a0
|
Almno10
2010-11-10 19:56:42 |
I don't think this is the definition of the bohr radius. The bohr model is classical.
The "come one, its bohr" argument is correct. The bohr model is very good despite its crappy, classical derivation.
|
walczyk
2011-04-07 20:55:37 |
Almno10: The brilliant thing about bohr is that he reached this result with his own proto-quantum mechanics, and thus the radius is named after him. go read a book
|
walczyk
2011-04-07 20:56:55 |
nvm, read it wrong and didn't mean to post a dick comment :/
|
|  | jax
2005-11-30 19:03:20 | Why does dV become  ? Isn't that the surface area ? ? Isn't that the surface area ?
yosun
2005-11-30 20:19:06 |
jax: thanks for the typo alert; the typo's been fixed: 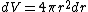 . (The radial probability distribution . (The radial probability distribution 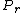 is related to the probability is related to the probability 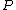 by by 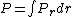 .) .)
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
