|
GR0177 #9
|
|
|
Problem
|
|
|
This problem is still being typed. |
Electromagnetism }Electric Field }Electric Field
From symmetry, one has 0-field at the center. This is choice (A).
Take the limit of an infinite number of charges placed around the center. In two dimensions, one has a circle of charges. This is similar to a 2-dimensional conductor. There is 0-electric-field inside a conductor (the potential is constant inside). But, for a less-than-infinite number of charges, one would only have 0-field in the center. Gauss' Law inside would have a gaussian surface (just a loop in 2-dimensions) surrounding 0 charge.
The brute-force way would be to compute the electric field via Coulomb's Law and vector addition. With the proper coordinates and a 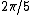 angle unit circle, this is a easy calculation. angle unit circle, this is a easy calculation.
|
|
|
Alternate Solutions |
BerkeleyEric
2010-07-11 17:36:59 | Consider some arbitrary electric field vector at the center of the circle. If it has a finite length, there are always four equivalent vectors (from rotation by 72 degrees) which correspond to the same physical situation. But the vector is uniquely defined, so it must be (A). |  |
|
|
Comments |
whereami
2018-04-06 14:20:34 | look at any regular polygon. draw the lines that connect each vertex to the center of the polygon. the lines themselves can form another regular polygon. This means their vector sum is zero. so is E. |  | Nebula
2015-09-18 21:47:40 | Expanding on the symmetry argument. Imagine rotating the 5 charges 72° CW or CCW. The system will look exactly the same. Therefore, there can\'t be an E field in the center, otherwise we could rotate the charges and come up with a different E field for the same configuration. |  | vasilis
2011-11-09 07:22:59 | The most transparent method is to consider the electric potential at the centre (since no vectors are involved).
Clearly each charge contributes the same V= kq/r^2 =constant; hence  = - div (V) = 0. = - div (V) = 0. |  | mianghazanfar786
2010-07-26 15:06:50 | According to 3rd application of Gauss's Law, the charge inside a hollow sphere is 0. Although a numbers of charges are spread over the sphere outside. so the choice is (A)
ahmedali__
2017-08-28 19:13:42 |
the answer is true but your justification is not. \r\nto solve an electrostatic problem using the potential, you should calculate it very generic at any point (r,theta,phi) in the three dimensional space or (r,theta) in two dimensional space, then take the derivative. \r\nwhat you\'ve done is you got the potential at specific point, so it is obviously will give you constant specif value, so if you apply this method to any configuration you will get zero field, and that is not true.
|
|  | BerkeleyEric
2010-07-11 17:36:59 | Consider some arbitrary electric field vector at the center of the circle. If it has a finite length, there are always four equivalent vectors (from rotation by 72 degrees) which correspond to the same physical situation. But the vector is uniquely defined, so it must be (A).
alece
2016-10-22 23:11:31 |
This is, in my opinion, the most elegant and intuitive solution.
|
|  | physicsworks
2010-02-06 02:17:41 | You can solve this problem not only for five or, say, eleven charges but for an arbitrary number of equal charges 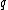 situated at the coners of a regular situated at the coners of a regular  -sided ploygon ( -sided ploygon ( is either odd or even number). is either odd or even number).
The solution to this problem is a sum of  vectors equal in length. Any two neighbors in this sum are separated by the angle vectors equal in length. Any two neighbors in this sum are separated by the angle  (so the picture of (so the picture of  vectors is like vectors is like  "sunbeams"). You can choose an arbitrary vector and project all the vectors on the line on which the first vector lies. If the length of the vectors is 1 you will get: "sunbeams"). You can choose an arbitrary vector and project all the vectors on the line on which the first vector lies. If the length of the vectors is 1 you will get:
\alpha,) where where 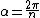 . .
There is such a nice formula:
\alpha) = \frac{sin(n-1/2)\alpha}{sin(\alpha/2)}) . Using this: . Using this:
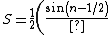\alpha}{sin(\alpha/2)} +1\right)= \frac{sin(n-1/2)\alpha + sin(\alpha/2)}{2sin(\alpha/2)}=\frac{sin(n\alpha/2) \cdot cos(n-1)\alpha/2}{sin(\alpha/2)})
Substituting 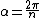 : :
 \cdot cos(n-1)\alpha/2}{sin(\alpha/2)}=0) for all for all  . .
So the projection of resulting field on the choosing line is zero. And since this line was arbitrary, one can conclude that electric field is zero.
frederic.c.brown
2011-10-27 08:16:45 |
I'm confused on where the cosine and sine equation above came from. Was this an trigonometry identity? What does S stand for?
|
frederic.c.brown
2011-10-27 08:19:34 |
I'm confused on where the cosine and sine equation above came from. Was this an trigonometry identity? What does S stand for?
|
buaasyh
2014-10-20 06:39:00 |
According to the product-to-sum identities, ![2cos[(n-1)\alpha]\,sin(\alpha/2)=sin(\frac{2n-1}{2}\alpha)-sin(\frac{2n-3}{2}\alpha)\,(n=2,\,3\,\cdots)](/cgi-bin/mimetex.cgi?2cos[(n-1)\alpha]\,sin(\alpha/2)=sin(\frac{2n-1}{2}\alpha)-sin(\frac{2n-3}{2}\alpha)\,(n=2,\,3\,\cdots)) , which will lead to progressive elimination in summation , which will lead to progressive elimination in summation ) . .
![\frac{sin[(n-1)\alpha/2]}{sin(\alpha/2)}](/cgi-bin/mimetex.cgi?\frac{sin[(n-1)\alpha/2]}{sin(\alpha/2)}) is the form of the Dirichlet kernel (see http://en.wikipedia.org/wiki/List_of_trigonometric_identities). is the form of the Dirichlet kernel (see http://en.wikipedia.org/wiki/List_of_trigonometric_identities).
|
|  | Tevatron
2009-10-25 18:34:07 | The solution should be (C) 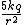
Remember that electric fields follow the principle of superposition. Each individual charge produces a field of  . The total electric field is the summation of all 5 of these fields. . The total electric field is the summation of all 5 of these fields.
Note that even if the charges were not distributed symmetrically about the circle, the net field at the center would still be C, as long as all 5 charges were on the circle.
CMSmonkey
2009-10-31 16:42:24 |
It is true that electric fields follow the principle of superposition, but remember that the fields do not all point in the same direction. So there will be "destructive" superposition. What you said may be applicable to the electric potential at the center - the potential is not a vector quantity.
|
Tevatron
2009-11-01 20:24:26 |
Agh. You're right. I dunno what I was thinking.
|
|  | rajendratimilsina
2008-10-23 18:15:27 | Gauss law states that , to find an electric field charge must enclosed by the surface area . so i think by symmetry there is zero electric field at the centre of the circular coil.
homa
2013-10-18 11:23:28 |
Gauss' law doesn't state that. Gauss' law states that the total electric flux of some gaussian surface is directly proportional to the total enclosed charge. If you have a system with just a single point charge, then there is electric field everywhere, no matter where you choose to look. The reason for zero electric field is due to symmetry arguments and superposition, not gauss' law.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
