|
GR0177 #88
|
|
|
|
|
Alternate Solutions |
2010-03-22 13:22:47 | Method of Elimination:
(A) Out since B field is obviously not zero.
(B), (D), (E) Out since they don't have correct units.
Ans: (C)
I found this the fastest way to attack this problem. |  | fcarter
2008-10-13 17:07:58 | Here is the fast way: It's all about limits. In the limit of theta approaching 2pi the circle becomes complete. The field of a circular loop is well known and you ought to have memorized it. The only answer that reduces properly in the limit is C.
hybridusmanus
2010-06-30 16:14:29 |
If we had 1/4 of a loop, then our B-field at P is 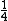 * * 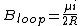
the fraction of the circle we have is: 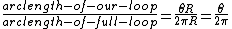
so the B-field at P is: ( \frac{\mu i}{2 R}) = \frac{\theta \mu i}{4\pi R}) , which is (C). , which is (C).
It is worth it to memorize the B-field of:
infinite wire
the center of a loop
inside a solenoid
inside a toroid
The magnetic field at a point of interest can be found using super position of all these geometries.
Here, we only have contribution from a fraction of a loop (circle), and not from the wires as they are in line with the point.
so we take the fraction of the loop length to a full circle and scale our magnetic field equation.
|
|  |
|
|
Comments |
2010-03-22 13:22:47 | Method of Elimination:
(A) Out since B field is obviously not zero.
(B), (D), (E) Out since they don't have correct units.
Ans: (C)
I found this the fastest way to attack this problem.
ken
2010-07-13 17:50:49 |
i think this is the easiest way to approach this problem as well
|
ncanna1
2010-09-25 12:14:50 |
(B) DOES have correct units. It only differs from (C) by a factor of 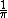 . .
|
Dodobird
2010-11-01 10:48:45 |
B has correct units.
|
aqme28
2010-11-09 18:38:57 |
B and C have the same units, so you can't discredit B based soley on this.
|
zero
2014-09-26 06:46:30 |
(B) and (C) have the same units
|
zero
2014-09-26 06:47:06 |
(B) and (C) have the same units
|
|  | sblmstyl
2008-10-15 21:57:49 | Should't this question be organized with the other EM questions? |  | fcarter
2008-10-13 17:07:58 | Here is the fast way: It's all about limits. In the limit of theta approaching 2pi the circle becomes complete. The field of a circular loop is well known and you ought to have memorized it. The only answer that reduces properly in the limit is C.
lattes
2008-10-13 19:33:31 |
Great solution!
|
Poop Loops
2008-11-02 00:52:51 |
I don't have it memorized and I can't find it anywhere. Help?
I know uI = B*2*pi*r for a wire, so B = uI/(2*pi*r).
But for answer C at Theta = 2*pi, B = uI/(2R).
So how do I get rid of that pi by itself?
|
zaijings
2009-03-31 14:51:38 |
the center B field of circular loop:
B=UI/2R
|
hybridusmanus
2010-06-30 16:14:29 |
If we had 1/4 of a loop, then our B-field at P is 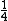 * * 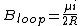
the fraction of the circle we have is: 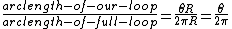
so the B-field at P is: ( \frac{\mu i}{2 R}) = \frac{\theta \mu i}{4\pi R}) , which is (C). , which is (C).
It is worth it to memorize the B-field of:
infinite wire
the center of a loop
inside a solenoid
inside a toroid
The magnetic field at a point of interest can be found using super position of all these geometries.
Here, we only have contribution from a fraction of a loop (circle), and not from the wires as they are in line with the point.
so we take the fraction of the loop length to a full circle and scale our magnetic field equation.
|
John777
2011-11-08 06:44:02 |
Nice response!
|
yummyhat
2017-10-27 03:46:41 |
thanks hybrid
|
|  | Richard
2007-10-29 11:45:27 | The Biot-Savart law for a 1d current:
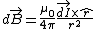
 is the distance from the point is the distance from the point 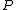 to the source. to the source.
As Yosun pointed out, the contributions due to the line currents are zero since 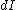 is in the same direction as is in the same direction as 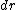 . To find the field due to the curved segment, notice that . To find the field due to the curved segment, notice that  is always perpendicular to is always perpendicular to 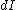 and integrate: and integrate:
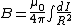
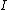 is a constant so is a constant so 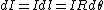
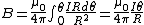
|  | Richard
2007-10-29 11:22:31 | How about this:
It's pretty clear that the magnetic field should be inversely proportional to 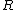 but proportional to but proportional to 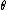 . .
Also, as you know from Ampere's law the field goes as 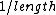 not not 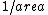 of an Amperian loop. This "means" there should be a of an Amperian loop. This "means" there should be a 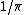 in the denominator. in the denominator.
Choice (C) fits....not all that solid I know. |  | globalphysics
2006-11-05 20:33:05 | I agree with the statement from the user above. Just a small detail: In the description of subject material it should be "Biot-Savart Law" not "Biot-Savert". Small thing. |  | herrphysik
2006-10-01 18:54:42 | Sorry for being so picky, but you should have 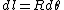 or or 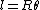 . I think I speak for every test-taker who finds his or her way to your site when I say your efforts are much appreciated. Thanks Yosun. . I think I speak for every test-taker who finds his or her way to your site when I say your efforts are much appreciated. Thanks Yosun. |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
