|
GR0177 #84
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
grephy
2012-11-06 09:39:13 | why s is not taken into account?
In transition C, there IS a change in s, right? Then why this transition can happen?!
jonrichens
2012-11-08 02:39:37 |
I believe that the spin selection rule only comes into play for multi-electron atoms (where the directional spin breaks the symmetry, or something). This question
is about hydrogen and the orientation of spin is not conserved in the same way.
Hydrogen selection rules
(delta)j = 0, +- 1 not 0 -> 0
(delta)l = +- 1
(delta)mj = 0, +- 1
Helium selection rule (spin orientation important)
(delta)j = 0, +- 1 not 0 -> 0
(delta)l = 0, +- 1
(delta)mj = 0, +- 1
(delta)s = 0 not 0 -> 0
hope that helps
|
|  | antithesis
2007-10-01 17:36:51 | Can you clarify?
You state the selection rules for l and m, but when you go through the ABC options, you only mentions the l and j rules (I know they are related).
Thanks
Richard
2007-10-30 11:12:31 |
The condition on the total angular momentum quantum number comes from the fact that
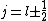
I think it may be best to remember that for an electric-dipole transition the following selection rules apply:
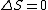
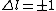
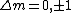
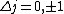
with the exception of a 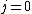 to to 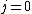 transition. transition.
Of course, these rules are different when you have a quadrupole or octupole transition. I believe the only difference is an additional 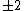 or or 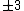 possibility on possibility on 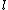 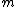 and and 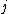 for quadrupole and octupole respectively. for quadrupole and octupole respectively.
|
|  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
