|
GR0177 #79
|
|
|
|
|
Alternate Solutions |
Deafro
2012-01-24 15:45:45 | E^2=sqrt(p^2*c^2+(m*c^2)^2)
E=10 GeV
p=8 GeV/c
mc^2= rest energy
Rearrange the formula and solve for mc^2. |  | mike
2009-11-06 18:34:27 | Another way of doing it:

and
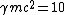 . Multiply the first eqn by . Multiply the first eqn by 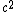 and divide the two to get: and divide the two to get:
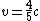
Plug in to 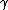 to find to find 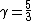 . .
Plug back in to the momentum equation:

thus 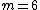 . .
I omit units, but it should be easy enough to follow. It seems a little longer, but its much less thinking once one remembers the relativistic energy/momenta equations. |  | Ning Bao
2008-02-01 07:43:40 | Set c=1 -> pythagorean triple. |  |
|
|
Comments |
Deafro
2012-01-24 15:45:45 | E^2=sqrt(p^2*c^2+(m*c^2)^2)
E=10 GeV
p=8 GeV/c
mc^2= rest energy
Rearrange the formula and solve for mc^2. |  | mike
2009-11-06 18:34:27 | Another way of doing it:

and
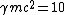 . Multiply the first eqn by . Multiply the first eqn by 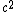 and divide the two to get: and divide the two to get:
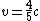
Plug in to 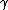 to find to find 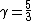 . .
Plug back in to the momentum equation:

thus 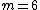 . .
I omit units, but it should be easy enough to follow. It seems a little longer, but its much less thinking once one remembers the relativistic energy/momenta equations. |  | astrodoo
2008-09-17 01:38:23 | manasi, the value of 64 (<- the square of momentum) has a dimension of 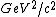 , so you can easily catch the yosun's solution if you consider the dimension of each terms. , so you can easily catch the yosun's solution if you consider the dimension of each terms. |  | Ning Bao
2008-02-01 07:43:40 | Set c=1 -> pythagorean triple. |  | Gaffer
2007-10-24 08:42:58 | There is a typo in the soln, which is why manasi is confused. Yosun used the  to cancel the GeV/c in the momentum. But then she pulled it out again inthe next line. to cancel the GeV/c in the momentum. But then she pulled it out again inthe next line.
No biggie.
It should go:
Plugging the momentum into the first equation, one has 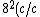^2 + m^2 c^4 = 10^2)
and then continue as she concludes |  | manasi
2007-09-28 12:05:48 | hi, if i m not mistaken shudnt it be 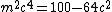 ???? ????
hope it appears rite m new to latex!!
hey thanks a lot yosun.. ur solutions are very helpful!! :)
astrodoo
2008-09-17 01:46:59 |
manasi, the value of 64 (<- the square of the momentum) has a dimension of 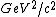 , so you can easily catch Yosun's solution in which , so you can easily catch Yosun's solution in which  term is disappeared if you look dimensions of each term. term is disappeared if you look dimensions of each term.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
