|
GR0177 #72
|
|
|
Problem
|
|
|
This problem is still being typed. |
Mechanics }Forces }Forces
Before the string is cut, one has the basic static equilibrium condition, for each block 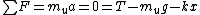 and and 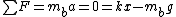 , where , where  refers to the upper block and refers to the upper block and  refers to the bottom block. Adding, one has refers to the bottom block. Adding, one has  a = 0 = T-m_ug - m_b) . .
After the string is cut, the tension goes to 0, but one has a non-zero net acceleration. The top mass has 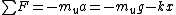 , where the minus sign comes in since the question wants the downward acceleration. The bottom mass has , where the minus sign comes in since the question wants the downward acceleration. The bottom mass has 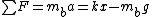 . But, immediately after the string is cut, the lower mass has 0 acceleration. Thus, . But, immediately after the string is cut, the lower mass has 0 acceleration. Thus, 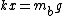 . Plugging this into the equation for the upper mass, one finds that . Plugging this into the equation for the upper mass, one finds that 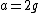 , as in choice (E). , as in choice (E).
|
|
|
Alternate Solutions |
testtest
2010-10-08 19:46:44 | Since none of the answers involve the spring constant, let it go to infinity. Then one can consider just the two blocks as a whole, with F = 2mg. Then one of the mass must have acceleration 2g (a = F/m = 2mg/m = 2g). |  | travis.nicholson
2006-10-27 13:24:38 | Try solving the problem like this:
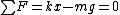 for the lower mass before the string breaks. for the lower mass before the string breaks.
Therefore, 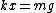 . .
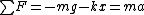 for the upper mass after the spring breaks. for the upper mass after the spring breaks.
Using the fact that 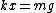 , ,
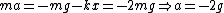
Therefore, the downward acceleration is 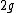 |  | erc
2005-11-10 13:44:38 | Could one also do this as follows:
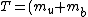g)
ie gravity acting on masses, neglecting the mass of the spring.
Since the masses are identical, this is just
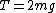
Then the force acting on the top mass is 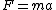
and this balances the tension, thus
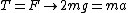
and thus
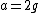 . .
travis.nicholson
2006-10-27 13:06:21 |
When you say "Then the force acting on the top mass is 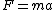 ," I assume that you began this sentence with "Then ..." in order to signify that you are talking about what happens after the string snaps. (My assumption arose from the fact that you have added a non-zero acceleration to your force equation.) ," I assume that you began this sentence with "Then ..." in order to signify that you are talking about what happens after the string snaps. (My assumption arose from the fact that you have added a non-zero acceleration to your force equation.)
However, after the string snaps, it is not true that 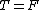 because there is no tension after the string breaks. because there is no tension after the string breaks.
|
|  |
|
|
Comments |
tweetiebird
2014-12-01 19:53:20 | it seems the author left a factor of (g) from one of the equations. |  | testtest
2010-10-08 19:46:44 | Since none of the answers involve the spring constant, let it go to infinity. Then one can consider just the two blocks as a whole, with F = 2mg. Then one of the mass must have acceleration 2g (a = F/m = 2mg/m = 2g). |  | mohammad.soly
2009-09-02 10:14:36 | The upper box is named 1 and the other 2. 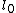 is free length of spring. I take the zero point of potential (U=0) at ceiling, so is free length of spring. I take the zero point of potential (U=0) at ceiling, so 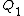 and and  are both negative : are both negative :
L = T - U =  - ( mg Q_1 + mg Q_2 + \frac{1}{2} k ( Q_1- Q_2-l_0)^2 ))
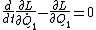
 = 0 )
Since : k ( 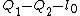 ) = k(delta x) = mg , thus : ) = k(delta x) = mg , thus :
 = 0 \Rightarrow \ddot{Q_1} = a_1 =- 2g) (answer) (answer)
and also we have for box 2 :
 = 0 \Rightarrow \ddot{Q_2} = a_2 = 0)
Camoph
2010-02-18 08:30:37 |
Good solution, but I'm not sure if you have time to do all this in the test, considering that you have 1,7min (average) for every question. Thank you indeed.
|
|  | GREview
2009-06-03 13:03:06 | I had trouble thinking about why 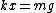 . Both the Lagrangian and the standard force balancing solutions rely on the above equation, and it's not readily obvious to me as to why the bottom mass has an initial zero acceleration. Here is an intuitive way that might help: . Both the Lagrangian and the standard force balancing solutions rely on the above equation, and it's not readily obvious to me as to why the bottom mass has an initial zero acceleration. Here is an intuitive way that might help:
When drawing force diagrams at equilibrium, one balances them so that 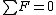 . So, for this system, before the string is cut, we have the spring trying to condense itself back to equilibrium, the two masses wanting to fall, and the string being the only thing standing between them and gravity. So (with $g>0$ defined) we have: . So, for this system, before the string is cut, we have the spring trying to condense itself back to equilibrium, the two masses wanting to fall, and the string being the only thing standing between them and gravity. So (with $g>0$ defined) we have:
Top mass
 = 0)
Bottom mass
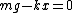
Now, after the string is cut, two things happen: tension goes to 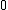 and everything starts to move. However, let's just concentrate on the tension: and everything starts to move. However, let's just concentrate on the tension:
Let 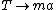 . Since . Since 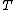 is no longer a force, it has to go somewhere, i.e., it has morphed into motion, or is no longer a force, it has to go somewhere, i.e., it has morphed into motion, or 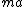 . Since there was no . Since there was no 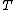 in the bottom equation, that doesn't change. Doing this allows us to write: in the bottom equation, that doesn't change. Doing this allows us to write:
Top mass
 = 0)
Bottom mass
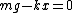
Now, we substitute the bottom mass into the top and obtain the desired solution: 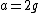 . .
I'm not sure whether this strategy of substitution works in general, and I would appreciate comments of any sort as to why it does or does not.
betelguese05
2012-10-12 16:40:12 |
I thought this problem was super easy. Draw the free-body diagram. There is gravity (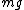 ) pulling on the first block as well as the weight of the second block (also ) pulling on the first block as well as the weight of the second block (also 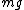 ). Balancing these is ). Balancing these is 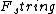 upward. Immediately after the string is cut, upward. Immediately after the string is cut, 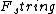 disappears so disappears so 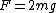 so so 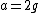 . .
|
|  | StrangeQuark
2007-05-17 10:54:01 | I have always been bad at dealing with forces. Energy is my thing, so I did this problem using the Lagrangian Formalisium, I find this way I am less likely to drop minus signs or make these kinds of mistakes;
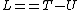
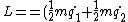-(-mq_1g-mq_2g+\frac{1}{2}(q_2-q_1)^2k)
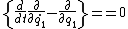
Now recall
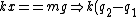==mg)
thus
==0)
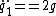
lmontanari
2008-09-14 20:50:45 |
Shouldn't the T term in the Lagrangian be (1/2 m(dq/dx)^2 + 1/2 m(dq/dx)^2).
In which case, the solution whould be g, not 2g.
I don't think this is the correct value for the energy of this system.
|
mohammad.soly
2009-09-02 09:56:52 |
The solution needs a little correction.
The upper box is named 1 and the other 2. 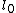 is free length of spring. is free length of spring.
I take the zero point of potential at ceiling, so 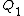 and and  are negative : are negative :
L = T - U =  - ( mg Q_1 + mg Q_2 + \frac{1}{2} k ( Q_1- Q_2-l_0)^2 ))
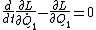
since k ( 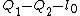 ) = k(delta x) = mg , thus : ) = k(delta x) = mg , thus :
m = 0 \Rightarrow \ddot{Q_1} = a_1 =- 2g)
and also we have for box 2 :
m = 0 \Rightarrow \ddot{Q_2} = a_2 = 0)
|
|  | travis.nicholson
2006-10-27 13:24:38 | Try solving the problem like this:
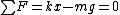 for the lower mass before the string breaks. for the lower mass before the string breaks.
Therefore, 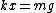 . .
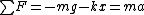 for the upper mass after the spring breaks. for the upper mass after the spring breaks.
Using the fact that 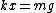 , ,
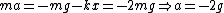
Therefore, the downward acceleration is 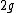
jonny23
2007-06-14 12:15:18 |
suka
|
jesford
2008-04-05 11:46:52 |
nice!
|
|  | travis.nicholson
2006-10-27 13:16:55 | The error in your reasoning occurs in the sentence "But, immediately after the string is cut, the lower mass has 0 acceleration. Thus, 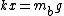 ." ."
You have assumed that the lower mass has a acceleration of zero and concluded that 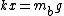 . This assumption is not generally true (if the masses are different), nor, in my opinion, is it intuitively obvious enough (in the case of equal masses) to merely be stated. . This assumption is not generally true (if the masses are different), nor, in my opinion, is it intuitively obvious enough (in the case of equal masses) to merely be stated.
However, it can be shown by analysis of  in its equilibrium state that in its equilibrium state that 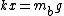 , and therefore the lower mass has an acceleration of 0 (but this reasoning cannot go in the other direction). , and therefore the lower mass has an acceleration of 0 (but this reasoning cannot go in the other direction). |  | erc
2005-11-10 13:44:38 | Could one also do this as follows:
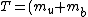g)
ie gravity acting on masses, neglecting the mass of the spring.
Since the masses are identical, this is just
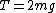
Then the force acting on the top mass is 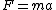
and this balances the tension, thus
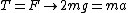
and thus
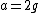 . .
erc
2005-11-10 13:47:28 |
Ah...sorry that comment came out such a mess... evidently not all latex commands are allowed. \rightarrow should give an "implies" sign.
Apologies.
|
yosun
2005-11-10 14:05:36 |
erc: all latex commands are allowed (math commands, that is). you just have to properly surround your equations with dollar-signs (one to start it and one to end it) or else the parser gets confused about which equations you want parsed. so  all work... among other things. i have manually corrected your post. all work... among other things. i have manually corrected your post.
|
travis.nicholson
2006-10-27 13:06:21 |
When you say "Then the force acting on the top mass is 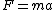 ," I assume that you began this sentence with "Then ..." in order to signify that you are talking about what happens after the string snaps. (My assumption arose from the fact that you have added a non-zero acceleration to your force equation.) ," I assume that you began this sentence with "Then ..." in order to signify that you are talking about what happens after the string snaps. (My assumption arose from the fact that you have added a non-zero acceleration to your force equation.)
However, after the string snaps, it is not true that 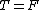 because there is no tension after the string breaks. because there is no tension after the string breaks.
|
FatheadVT
2010-11-11 17:18:43 |
Second this solution. It's clear that before cutting the rope, the net downard force on the block is 2mg which is counteracted by T = 2mg. When the tension is removed from the block, the spring continues to pull down so the net downward force is still 2mg and the net force is 2mg. Great solution.
|
|  |
|
| Post A Comment! |
You are replying to:
I had trouble thinking about why 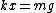 . Both the Lagrangian and the standard force balancing solutions rely on the above equation, and it's not readily obvious to me as to why the bottom mass has an initial zero acceleration. Here is an intuitive way that might help:
When drawing force diagrams at equilibrium, one balances them so that 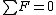 . So, for this system, before the string is cut, we have the spring trying to condense itself back to equilibrium, the two masses wanting to fall, and the string being the only thing standing between them and gravity. So (with $g>0$ defined) we have:
Top mass
 = 0)
Bottom mass
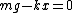
Now, after the string is cut, two things happen: tension goes to 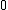 and everything starts to move. However, let's just concentrate on the tension:
Let 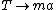 . Since 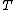 is no longer a force, it has to go somewhere, i.e., it has morphed into motion, or 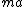 . Since there was no 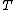 in the bottom equation, that doesn't change. Doing this allows us to write:
Top mass
 = 0)
Bottom mass
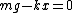
Now, we substitute the bottom mass into the top and obtain the desired solution: 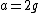 .
I'm not sure whether this strategy of substitution works in general, and I would appreciate comments of any sort as to why it does or does not.
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
