|
GR0177 #71
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
anGRE
2016-10-26 12:01:38 | This problem is just misleading. The observer measures the wavelengths to a precision of four significant digits, but the answer choices are only stated to two significant digits. It should say MOST NEARLY somewhere in the problem statement. I failed to solve the problem under testing conditions because of the poor phrasing. \r\n\r\nIn case anyone is interested in my method:\r\n\r\nThe ratio 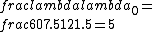 , exactly. So I was expecting nice numbers to fall out of the calculation.\r\n\r\nNoting that this is a redshift, and that in general stuff doesn\'t move faster than c, I narrowed to choices (C) and (D).\r\n\r\nInstead of solving the equation for beta, which I worry might end in a nasty quadratic, I plug these two choices in as fractions of c to the equation for the relativistic doppler shift:\r\n\r\nFor (C), , exactly. So I was expecting nice numbers to fall out of the calculation.\r\n\r\nNoting that this is a redshift, and that in general stuff doesn\'t move faster than c, I narrowed to choices (C) and (D).\r\n\r\nInstead of solving the equation for beta, which I worry might end in a nasty quadratic, I plug these two choices in as fractions of c to the equation for the relativistic doppler shift:\r\n\r\nFor (C), }{1-(12/15)}} = 3) \r\nFor (D), \r\nFor (D), }{1-(14/15)}} = sqrt{29}) \r\n\r\nRemember, I expect to see a nice round 5. Obviously root 29 is closer, but given the precision to which the wavelengths are stated, I expect to land on one of the answer choices exactly. So I conclude I either have made an algebra error, or I misremembered the doppler shift formula. I mark no answer choice.\r\n\r\nIt\'s crazy that 32% of people who took the exam got this question correct. Arriving at the correct answer involves an unwarranted approximation at best and a math error at worst.\r\n\r\n \r\n\r\nRemember, I expect to see a nice round 5. Obviously root 29 is closer, but given the precision to which the wavelengths are stated, I expect to land on one of the answer choices exactly. So I conclude I either have made an algebra error, or I misremembered the doppler shift formula. I mark no answer choice.\r\n\r\nIt\'s crazy that 32% of people who took the exam got this question correct. Arriving at the correct answer involves an unwarranted approximation at best and a math error at worst.\r\n\r\n
anGRE
2016-10-26 12:04:05 |
Wow, the formatting totally got fucked. All of the forward slashes just disappeared. Rough.\r\n\r\nWell I spent enough time on this. Just ignore it.
|
|  | johnVay
2013-10-16 17:12:06 | do this problem first without considering gamma -- you'll get a or c, recognize that you're getting redshifted, so eliminate a. then recognize that you're nearing the speed of light, so you need a boost from gamma. so boost to d. |  | walczyk
2011-04-07 18:37:43 | pardon my language but how the fuck are people getting values of 6??.. you observe a wavelength 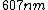 , and know that the line is , and know that the line is 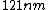 ... ...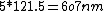 .... ....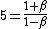 ... ... 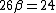 ... ... 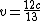 Why do people use six instead of five! Why do people use six instead of five!
gremonkey
2011-11-11 17:40:58 |
either way, the answer is the same. both 35/37 and 12/13 are close to 2.8, but yes it should be 5 instead
|
UNKNOWNUMBER
2018-10-20 00:12:35 |
We use 6 instead of 5 because we approximate 121.5 nm as 100 nm and 607.5 nm as 600 nm. 600/100 = 6.
|
|  | Camoph
2010-02-18 08:24:02 | I like your idea about using common, and it works I think, however answers B and c are very close. In the moment of the test, under pressure, is really hard try to deicide between them. There is a way to make a basic caculation to get the right answer between B and C ?
hybridusmanus
2010-06-28 18:52:27 |
I think you should eliminate A,B, and E from the beginning:
First, asses whether it's coming at you, or traveling away;
when a car travels AT you, it sounds HIGHER pitched--higher pitch means SHORTER wave length
_____________Towards Observer_|_Away from
Pitch (frequency) : _____high______|__low___
____Wavelength : _____short_____|__long___
So, coming towards leaves C, D, E
and E is faster than c, so it can be eliminated. Then using
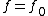 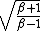
*note: Switch the signs when needed: + will make the top larger, a larger frequency is higher pitched (coming at you),...
Solve for 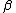
|
|  | istezamer
2009-11-01 16:21:53 | Actually I solved this a little bit different!! I used No calculations!!
Since the wavelength has elongated then one must assume that the velocity is away from earth "Red-Shift" This eliminates choices A & B
Choice E is certainly out because it is a speed larger than c..
The Elongation is obviously large !! 6 times the initial length.. This means that the speed must be closer to c.. which yields choice D.
I Try to solve most of the problems using common sense and it works!! I guess the trick to score good in this exam is to go quick!
physicsman
2010-02-17 15:41:57 |
So 2.8 is close but 2.4 isnt?
|
Camoph
2010-02-18 08:22:12 |
I like your idea about using common sense, and it works, however, in this case the answers B and C are very close, in the moment of the test, under pressure is very hard try to deicide about one of them. There is an alternative way to do some basic calculation to give the right answer, beteween B and C?
|
Camoph
2010-02-18 08:26:13 |
Sorry, I mean answers C and D.
|
buaasyh
2015-10-13 07:29:12 |
Here is a way to distinguish between 2.4 and 2.8. Solve the relativistic Doppler shift relation and get v=(24/26)*c. If the denominator is 30, v equals 2.4. The denominator is 26, a little less than 30, so v is a little bigger than 2.4. Thus 2.8 is the choice.
|
|  | Poop Loops
2008-11-01 20:35:17 | What the hell is a "radial velocity"? I had the answer perfect and then I decided to multiply it by  because it was "radial" and got E. because it was "radial" and got E.
Jeremy P
2008-11-03 14:36:57 |
In spherical coordinates, as opposed to Cartesian coordinates, radial is toward or away from the earth (which is spherical).
|
jmracek
2009-10-20 13:16:24 |
(E) could not have been the right answer because that would mean the planet is moving faster than the speed of light, obviously impossible.
|
Albert
2009-10-28 17:20:04 |
The planets and galaxies can indeed move near or even faster than the speed of light. Getting a signal from such a galaxy is not only possible but rather practised regularly for various things in Astronomy. Refer to the link to get more details. Thanks
http://curious.astro.cornell.edu/question.php?number=575
|
llama
2013-10-14 02:29:17 |
I think Albert's statement is very misleading, since it's impossible to get a redshift value that implies v>c (as  -> -> 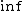 as as  -> ->  ), and you'll never get an answer with v>c in a question of this type. ), and you'll never get an answer with v>c in a question of this type.
|
|  | petr1243
2008-04-07 16:52:42 | Source is moving away from the reciever, if:
 > >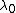 or f < f_0 or f < f_0
Source is moving toward the observer, if:
 < <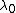 or f>f_0 or f>f_0
|  | hisperati
2007-10-27 01:37:06 | This question implies the interpretation that distant objects in the universe are just receding from us, but getting an answer faster than the speed of light is ok! It is cosmology. Ned Wright's page, "Acutally However, if we assume that the distance of an object at time t is the distance from our position at time t to the object's position at time t measured by a set of observers moving with the expansion of the Universe, and all making their observations when they see the Universe as having age t, then the velocity (change in D per change in t) can definitely be larger than the speed of light. This is not a contradiction of special relativity because this distance is not the same as the spatial distance used in SR, and the age of the Universe is not the same as the time used in SR." Basically distant objects have a redshift, or Z , and that should be interpretted as what it is (which depends on the assumed properties of the universe, like curvature density, etc.) not necessarily a velocity. ETS doesn't ask perfect questions.
FatheadVT
2010-11-11 17:13:37 |
Ahh, but the GRE is by no means meant to select for good physicists! It's a great way to select for people who are really good at the physics GRE. The key here is memorizing, not thinking. Clear thinking is a disadvantage.
|
|  | grep
2006-10-31 20:29:29 | If you happen to've forgotten the relativistic doppler shift (like me) and are reduced to using the non-relativistic version, you get an answer like 4c. Obviously this has some level of inaccuracy when used at these velocities, but it is accurate enough at least to say that v is darn near the speed of light and take a guess at D.
Gaffer
2007-10-23 14:42:42 |
The 4c answer is option E to trip up those of us not clever enough to realize that 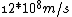 is greater than c. is greater than c.
|
|  | grep
2006-10-31 20:26:56 | |  | Andresito
2006-03-08 18:47:38 | Yosun, the ratio as pointed out above is exactly 5, even with an approximation one can say lamba/lamba0=61/12=5
Furthermore, this gives beta=4/4.2 ~~0.9
Thus v = beta*c = c = 2.8 E+8 m/s
Cheers, and thank you for the site |  | ee7klt
2005-11-11 12:01:22 | actually, 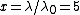 exactly. then exactly. then 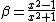 . . |  |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
