curious_onlooker
2017-10-25 19:29:58 | I\\\\\\\'m late to the party, but I think one way to distinguish between C and D is that the answer should be the same for + and - x. C does not have this property, so choose D. |  |
Baharmajorana
2014-09-19 12:41:36 | The circle's radius is 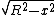 then it's cross section is then it's cross section is ) |  |
FatheadVT
2010-11-11 16:36:07 | Why is the answer not (E)? 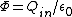 . If it's a surface charge, then there will be charges on both surfaces, so . If it's a surface charge, then there will be charges on both surfaces, so 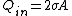 . That gives you (E) . That gives you (E) |  |
jmracek
2009-03-13 15:00:08 | The flux of electric field through the Gaussian surface will equal the sum of the charge inside divided by the permittivity. In this case, we have sheet charge of density  . To find the charge inside the sphere, you find the area of the circle formed by the intersection of the plane with the Gaussian surface then multiply by the charge density: . To find the charge inside the sphere, you find the area of the circle formed by the intersection of the plane with the Gaussian surface then multiply by the charge density:
 \sigma)
So that:
 \sigma}{\epsilon})
Yurlungur
2012-04-01 20:45:27 |
This is the best answer, and I think it's what ETS was looking for.
|
|  |
ATL
2008-11-07 13:32:36 | Gauss's law states that 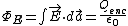 . .
The flux should be zero when 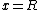 , which eliminates choices A and B. , which eliminates choices A and B.
The flux should be a maximum when 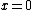 , which eliminates choice C. , which eliminates choice C.
When 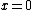 the enclosed charge is the enclosed charge is  , therefore the correct answer is D. , therefore the correct answer is D.
Crand0r
2010-11-10 19:47:37 |
The expression in answer C, ^{2}\sigma}{\epsilon_0}) , is also a maximum at x = 0. , is also a maximum at x = 0.
To eliminate C, you could consider that the first derivative of 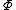 should be 0 when x is 0. At that point, I think just doing the problem in a straight-forward manner is faster if you remember how. should be 0 when x is 0. At that point, I think just doing the problem in a straight-forward manner is faster if you remember how.
|
calvin_physics
2014-04-03 19:28:29 |
Choice C gives you maximum flux as well at x = 0.
I eliminated everything else except C and D, and I didn't know which to choose from.
|
|  |
duckduck_85
2008-11-04 22:25:28 | I agree with vbphysics. I think the solution should be changed to show that the E field of an infinite plane is in fact 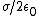 and that the 2 cancels out of the denominator when one considers both sides of the circle (as one needs to do when calculating the E field of the inf plane). and that the 2 cancels out of the denominator when one considers both sides of the circle (as one needs to do when calculating the E field of the inf plane). |  |
wangjj0120
2008-10-28 08:03:24 | I don't understand, since flux is 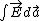 , here d , here d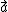 is in direction of r (r of the sphere), and direction of is in direction of r (r of the sphere), and direction of  is perpendicular to the sheet, that means there is always an angle between d is perpendicular to the sheet, that means there is always an angle between d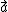 an an  , except at the point that d , except at the point that d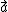 is perpendicular to the sheet. In this case, how can you just multiply E by is perpendicular to the sheet. In this case, how can you just multiply E by ) ? ?
Cosmo
2008-11-07 14:21:52 |
Consider an upside down hemispherical bowl of radius R at the origin with a charged sheet in the x-y plane. What is the flux through the outer surface of the hemisphere (the bowl shaped part as opposed to the flat circle part)? We know  is perpendicular to the sheet and that d is perpendicular to the sheet and that d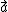 is in the direction of r. So there will be an angle between is in the direction of r. So there will be an angle between  and d and d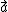 . But we also know that the flux going through the hemispherical surface of the bowl is equal to the amount of flux that goes into the flat circular part of the hemisphere. This is easier to calculate since d . But we also know that the flux going through the hemispherical surface of the bowl is equal to the amount of flux that goes into the flat circular part of the hemisphere. This is easier to calculate since d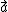 will be anti parallel to will be anti parallel to  . The area is that of a circle of radius R and the angle is always . The area is that of a circle of radius R and the angle is always  . .  = -1) so the flux is just so the flux is just  )   R^2 where R^2 where  is the magnitude of the electric field above the sheet. This is the flux going into the bowl so the flux coming out is the negative of the answer. So, for this problem it is the same concept except instead of having a hemisphere, the sphere was slice at a different place by the sheet. So it is the same idea except the flat circle part of the gaussian surface where the sheet cuts through does not have a radius of R but is the magnitude of the electric field above the sheet. This is the flux going into the bowl so the flux coming out is the negative of the answer. So, for this problem it is the same concept except instead of having a hemisphere, the sphere was slice at a different place by the sheet. So it is the same idea except the flat circle part of the gaussian surface where the sheet cuts through does not have a radius of R but 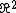 - -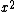
|
Moush
2010-09-18 11:59:51 |
Excellent description by Cosmo. Definitely clears things up.
|
|  |
awhitbe2
2006-06-21 16:50:39 | I agee with the above comment. However I feel there is clarification needed (I did not feel this was obvious).
The plane intersect the circle at a distance x from the center. The gaussian surface marks a circle around the plane with radius (R^2-x^2)^1/2 by the pyth. theor. For surface density mult. sigma by area to get total charge. So you get the desired
pi*(R^2-x^2)*sigma/epsilon |  |
alpha
2005-12-31 22:43:56 | testing 123 italics
alpha
2005-12-31 22:54:21 |
testing 123 it
|
alpha
2005-12-31 22:56:15 |
testing 123 it again!
|
alpha
2005-12-31 22:56:32 |
grrr
|
alpha
2005-12-31 22:58:13 |
again!
|
alpha
2005-12-31 23:20:51 |
ZOOK
|
ali
2006-01-02 01:27:21 |
testing
|
|  |
vbphysics
2005-12-14 12:18:03 | There is a problem here.
1st the plane is never stated as conducting.
2nd you have two surfaces, albeit of equal size that will contribute to the flux.
) should equal sigma/(2 * epsilon) by gauss's law. When you plug that field into the integral, and solve for the flux coming through 2 circles of radius should equal sigma/(2 * epsilon) by gauss's law. When you plug that field into the integral, and solve for the flux coming through 2 circles of radius ) (one for each side of the sphere) you will get the right answer. (one for each side of the sphere) you will get the right answer.
An alternate way to examine this problem is to ignore the ) all together Gauss's law says that the flux through s simply connected gaussian surface IS the charge inside divided by epsilon. Therefore all you need is to know is Q = sigma * pi *(R^2-x^2). So flux = sigma * pi* (R^2-x^2)/epsilon. all together Gauss's law says that the flux through s simply connected gaussian surface IS the charge inside divided by epsilon. Therefore all you need is to know is Q = sigma * pi *(R^2-x^2). So flux = sigma * pi* (R^2-x^2)/epsilon.
Sorry about the sloppy LaTeX, I'm still learning.
Blake7
2007-09-21 19:55:53 |
All ETS is looking for here is a circle with surface charge on it enclosed in a spherical "gaussian" (Gauss's law) surface.
The size of the circle gives one the amount of enclosed charge. The trig gives you the size of the circle. No muss no fuss; not any more complicated than that.
|
|  |
