|
GR0177 #59
|
|
|
|
|
Alternate Solutions |
| There are no Alternate Solutions for this problem. Be the first to post one! |
|
|
Comments |
theperiodictable
2014-10-23 11:05:59 | One good thing to consider for this problem is the following: the only thing you can have a derivative of is x, since m and k are constants, so Q must be x. |  | bslugger360
2013-08-11 16:21:51 | Another thought that helped me was looking at the energy of a spring and the energy of a capacitor:
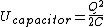
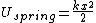
From this it's pretty clear that Q x and C x and C 1/k, making B the only possible answer. 1/k, making B the only possible answer. |  | mrTrig
2010-11-09 00:43:49 | Something nice to remember  for LC Circuits. And from hook's for LC Circuits. And from hook's 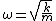 . Thus L and C must be inversely related and must be related to either . Thus L and C must be inversely related and must be related to either 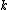 or or 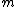 . Only B satisfies. . Only B satisfies. |  | carl_the_sagan
2008-11-07 19:48:26 | A really cheesy way is to totally disregard the question and just look at the answers. Typically on a question like this they are going to have to repeat the correct value for each column a few times.
so "m" is repeated in L, "1/k" is repeated in C, and "x" is repeated in Q. The only answer which lines all these multiple-occurring rows is B.
Granted this has nothing to do with physics, but this isn't about physics, its about getting the right answer.
amber
2014-10-22 23:27:03 |
I went with this route too. I figured if there were two that were close I could reason it out, but I didn't have to do that.
|
UNKNOWNUMBER
2018-10-18 21:06:34 |
I don\'t think this works all the time--I would say you just got lucky.
|
|  |
|
| Post A Comment! |
|
|
Bare Basic LaTeX Rosetta Stone
|
LaTeX syntax supported through dollar sign wrappers $, ex., $\alpha^2_0$ produces  . .
|
| type this... |
to get... |
| $\int_0^\infty$ |
 |
| $\partial$ |
 |
| $\Rightarrow$ |
 |
| $\ddot{x},\dot{x}$ |
 |
| $\sqrt{z}$ |
 |
| $\langle my \rangle$ |
 |
| $\left( abacadabra \right)_{me}$ |
_{me}) |
| $\vec{E}$ |
 |
| $\frac{a}{b}$ |
 |
|
|
|
|
The Sidebar Chatbox...
Scroll to see it, or resize your browser to ignore it... |
|
|
|
